


Nächste Seite: Dichteschwankungen des idealen Gases
Aufwärts: Statistische Physik, SS 2004
Vorherige Seite: Kanonische Verteilung aus der
Man hat für die großkanonische Gesamtheit
Die Summe über die Zustände kann als eine Doppelsumme über die
Teilchenzahlen und Energien aufgefasst werden:
wobei 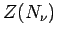 die Kanonische Zustandssumme für ein System mit
festem Teilchenzahl
die Kanonische Zustandssumme für ein System mit
festem Teilchenzahl 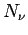 ist. So gilt z.B. für die Maxwell-Boltzmann
Statistik (klassische Teilchen)
ist. So gilt z.B. für die Maxwell-Boltzmann
Statistik (klassische Teilchen)
mit
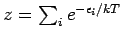 .
.
Beispiel: Ideales Gas:
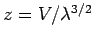 mit (
mit (
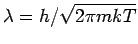 ) und
) und
![\begin{displaymath}
Z=\sum_{N}\frac{1}{N!}\left( e^{\mu /kT}z\right) ^{N}=\exp \...
...{\mu /kT}V \left( \frac{2\pi mkT}{h^{2}}
\right)^{3/2}\right]
\end{displaymath}](img269.png) |
(6) |
Folglich
![\begin{displaymath}
\Omega =-pV=-kT\ln Z=-kT\left[ e^{\mu /kT}V \left( \frac{2\pi mkT}{h^{2}}
\right)^{3/2}\right]
\end{displaymath}](img270.png) |
(7) |

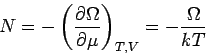 |
(8) |
d.h. 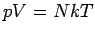 , und
, und
Weiterhin folgt aus Gl.(7), dass
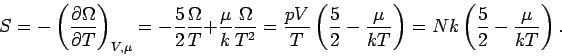 |
(9) |
Daher gilt:
Aus Gl.(7) folgt auch, dass

![\begin{displaymath}
\mu (T,p)=-kT\ln \left[ \left( \frac{2\pi \mu }{h^{2}}\right)
^{3/2}(kT)^{5/2}/p\right] .
\end{displaymath}](img277.png) |
(10) |
Eingesetzt in Gl.(9) ergibt das
die bekannte Sakur-Tetrode Gleichung.
Unterabschnitte



Nächste Seite: Dichteschwankungen des idealen Gases
Aufwärts: Statistische Physik, SS 2004
Vorherige Seite: Kanonische Verteilung aus der
Prof. Igor Sokolov
2004-07-01
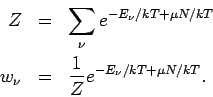
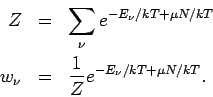
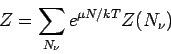
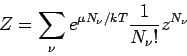
![]() mit (
mit (
![]() ) und
) und
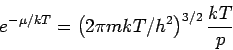
![\begin{eqnarray*}
S &=&Nk\left( \frac{5}{2}-\frac{\mu }{kT}\right) \\
&=&Nk\ln ...
...frac{2\pi mkT}{h^{2}}\right) ^{3/2}e^{5/2}\frac{V}{N}%
\right] ,
\end{eqnarray*}](img278.png)