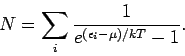Nächste Seite: Fermi-Dirac Statistic
Aufwärts: Exakte Statistik nichtwechselwirkender Teilchen
Vorherige Seite: Exakte Statistik nichtwechselwirkender Teilchen
(Satyendra Nath Bose (1924) für Photonen, A. Einstein für massive
Teilchen, 1925)
Voraussetzung: Bosonen (Teilchen mit ganzzahligen Spin), nicht durch das
Pauli-Verbot eingeschränkt. Beispiele: Photonen, Phononen, He -Atome,...
-Atome,...
Annahme: Nichtwechselwirkende Teilchen  ideale Bose-Gas.
ideale Bose-Gas.
Seien die Einteilchen-Energieniveaus 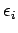 . Ein Zustand
. Ein Zustand 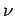 des
Systems ist durch die Besetzungszahlen
des
Systems ist durch die Besetzungszahlen 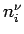 definiert (
definiert (
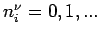 ). Teilchen sind ununterscheidbar, ihre Gesamtzahle
). Teilchen sind ununterscheidbar, ihre Gesamtzahle
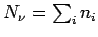 und die Gesamtenergie
und die Gesamtenergie
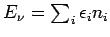 in Zustand
in Zustand 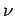 sind fixiert. Die großkanonosche Zustandssumme lautet:
sind fixiert. Die großkanonosche Zustandssumme lautet:
Die Summe über 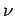 geht über alle Möglichkeiten, die
Besetzungszahlen
geht über alle Möglichkeiten, die
Besetzungszahlen 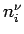 auszuwählen, so daß alle mögliche
Kombinationen von
auszuwählen, so daß alle mögliche
Kombinationen von
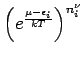 aufsummiert sind. Somit
aufsummiert sind. Somit
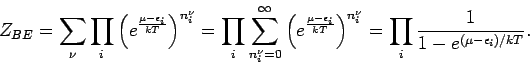 |
(11) |
Die Geometrische Reihe konvergiert nur wenn
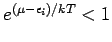 ,
d.h.
,
d.h.
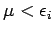 für alle Einteilchenzustände
für alle Einteilchenzustände 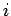 . Aus Gl.(11) folgt:
. Aus Gl.(11) folgt:
-
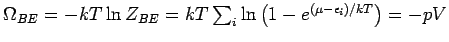
-
![$N=\sum_{i}n_{i}=-\left( \partial \Omega /\partial \mu \right)
_{T,V}=\sum_{i}\l...
...^{(\mu -\epsilon _{i})/kT}/\left( 1-e^{(\mu -\epsilon
_{i})/kT}\right) \right] $](img308.png)

Mittlere Besetzungszahl des Einteilchenniveaus 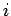 ist
ist
Wenn wir die Energie des Grundzustandes gleich 0 setzen, so ist es 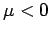 .
.



Nächste Seite: Fermi-Dirac Statistic
Aufwärts: Exakte Statistik nichtwechselwirkender Teilchen
Vorherige Seite: Exakte Statistik nichtwechselwirkender Teilchen
Prof. Igor Sokolov
2004-07-01
![]() -Atome,...
-Atome,...
![]() ideale Bose-Gas.
ideale Bose-Gas.
![]() . Ein Zustand
. Ein Zustand ![]() des
Systems ist durch die Besetzungszahlen
des
Systems ist durch die Besetzungszahlen ![]() definiert (
definiert (
![]() ). Teilchen sind ununterscheidbar, ihre Gesamtzahle
). Teilchen sind ununterscheidbar, ihre Gesamtzahle
![]() und die Gesamtenergie
und die Gesamtenergie
![]() in Zustand
in Zustand ![]() sind fixiert. Die großkanonosche Zustandssumme lautet:
sind fixiert. Die großkanonosche Zustandssumme lautet:
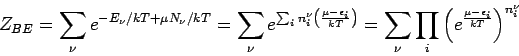
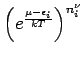 aufsummiert sind. Somit
aufsummiert sind. Somit