(E. Fermi, 1926; der Zusammenhang mit der Quantenmechanik wurde vom P.M. Dirac
geklärt (1926)). Voraussetzung: Fermionen (Teilchen mit halbzahligen
Spin). Pauli-Verbot ![]() die Besetzungszahlen der
Einteilchenzustände sind entweder 0 oder 1:
die Besetzungszahlen der
Einteilchenzustände sind entweder 0 oder 1:
![]() oder 1.
Beispiele: Elektronen, Protonen, He
oder 1.
Beispiele: Elektronen, Protonen, He![]() -Atome. Die Großkanonische
Zustandssumme lautet:
-Atome. Die Großkanonische
Zustandssumme lautet:
![\begin{displaymath}
Z_{FD}=\sum_{\nu }e^{-E_{\nu }/kT+\mu N_{\nu }/kT}=\prod_{i}...
...^{\nu
}}=\prod_{i}\left[ 1+e^{(\mu -\epsilon _{i})/kT}\right]
\end{displaymath}](img314.png)
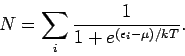
Bemerkung: Für klassische Teilchen (Maxwell-Boltzmann Statistik) erhält man
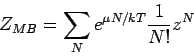
![\begin{displaymath}
Z_{MB}=\exp \left( e^{\mu /kT}z\right) =\exp \left[ \sum_{i}...
...ht] =\prod_{i} \exp\left[ e^{(\mu -\epsilon
_{i})/kT}\right] .
\end{displaymath}](img322.png)
Die mittlere Besetzungszahl des Einteilchenniveaus ![]() ist
ist