Photonen

Quantisierung der Eigenschwingungen des elektromagnetischen Feldes eines Hohlraumresonators. ${\mathbf p}=\hbar {\mathbf k}$, mit

$${\mathbf k} = \frac{2 \pi}{L_\alpha}, \quad \alpha=x, y, \mbox{ oder } z.$$

Die Energie jeder Schwingungsmode ist:

$$\epsilon_n ({\mathbf k}) = \hbar c k \left( n + \frac{1}{2} \right)$$

($n$ - Anzahl der Photonen in mode ${\mathbf k}$).

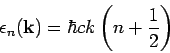
Erklärung: Das Feld oder die Potentiale, die analog zur Wellemfunktion betrachtet werden können, gehörchen der Wellengleichung

$$\frac{\partial ^2 \psi}{\partial t^2} = c^2 \Delta \psi.$$

In $k$-Darstellung $\psi(\mathbf r,t) \rightarrow \psi(\mathbf k,t)e^{i \mathbf{ kr }}$. Die Gleichung für $\psi(\mathbf k,t)$,

$$\frac{d^2}{dt^2} \psi(\mathbf k,t) = -k^2 c^2 \psi(\mathbf k,t)$$

ist die Gleichung für einen harmonischen Oszillator, und kann gleichermassen quantisiert werden.

Jeder Zustand ist zweifach entartet: Die 2 möglichen Spineinstellungen entsprechen links- oder rechts- zirkularpolarisierter elektromagnetischen Wellen mit vorgegebenen $\mathbf k$.

Das System nicht wechselwirkender Photonen kann als ideales Bose-Gas betrachtet werden.

Wichtig: Das Gleichgewicht zwischen dem Photonengas und dem Wärmebad (Körper mit dem Hohlraum) entsteht durch Emission und Absorbtion der Photonen. Die Gesamtzahl der Photonen $N$ ist daher keine Erhaltungsgrösse. Im GG stellt sich $N$ derart ein, dass die Freie Energie $F$ bei vorgegebenen $T$ und $V$ minimal wird, d.h. $(\partial F / \partial N)_{T,V} = 0$ und $N=N(T,V)$. Da $(\partial F / \partial N)_{T,V} = \mu$, haben wir stets $\mu=0$ und $\sigma = \exp (\mu / kT)=1$ und damit starke Entartung.

Bemerkung: Trotzdem findet keine Bose-Einstein Kondensation wegen des linearen Dispersionsgesetzes statt: Andere Form der $D(p)$!