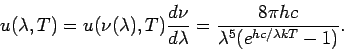Nächste Seite: Zustandsgleichung des Photonengases
Aufwärts: Photonen und Phononen
Vorherige Seite: Photonen
Sei 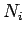 die mittlere Anzahl der Photonen der Schwingungsmode
die mittlere Anzahl der Photonen der Schwingungsmode  . Anhand der
Boseverteilung
. Anhand der
Boseverteilung
Gesamtzahl der Photonen
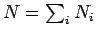 . Nach dem Kontinuumübergang erhält
man
. Nach dem Kontinuumübergang erhält
man
oder, als Funktion der Frequenz,
Die Interpretation:
mit:
und
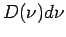 ist die Anz. der Zustände im Intervall
ist die Anz. der Zustände im Intervall
![$[\nu,\nu+d\nu]$](img460.png) .
Energie des Photonengases (ohne Nullpunktenergie)
.
Energie des Photonengases (ohne Nullpunktenergie)
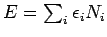 .
In kontinuierlicher Darstellung
.
In kontinuierlicher Darstellung
Definition:
mit 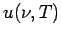 - Energiedichte pro Frequenzeinheit:
- Energiedichte pro Frequenzeinheit:
(PLANCK'sches Strahlungsgesetz).
Die gesamte Energiedichte ergibt sich als
Die Energie, die durch ein kleines Loch pro Zeiteinheit ausgeschtrahlt wird,
ist proportional zu 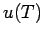 . Daher folgt für die Intensität der Strahlung
. Daher folgt für die Intensität der Strahlung
das STEFAN-BOLTZMANN-Gesetz.
Sei nun 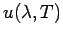 die Energiedichte der Strahlung pro Wellenlängeneinheit,
die Energiedichte der Strahlung pro Wellenlängeneinheit,
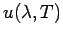 hat ihr Maximum bei der Wellenlänge
hat ihr Maximum bei der Wellenlänge
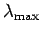 das
durch das WIENER'sches Verschiebungsgesetz gegeben ist:
das
durch das WIENER'sches Verschiebungsgesetz gegeben ist:
(hier ist 4.965... eine Wurzel der transzedenten Gleichung 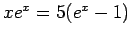 ).
Das Maximum der Strahlung verschiebt sich bei höheren Temperaturen zu
kürzeren Wellenlängen.
).
Das Maximum der Strahlung verschiebt sich bei höheren Temperaturen zu
kürzeren Wellenlängen.



Nächste Seite: Zustandsgleichung des Photonengases
Aufwärts: Photonen und Phononen
Vorherige Seite: Photonen
Prof. Igor Sokolov
2004-07-01
![]() die mittlere Anzahl der Photonen der Schwingungsmode
die mittlere Anzahl der Photonen der Schwingungsmode ![]() . Anhand der
Boseverteilung
. Anhand der
Boseverteilung
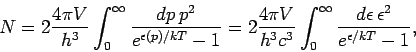
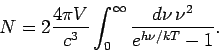
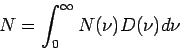
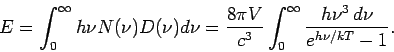
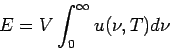
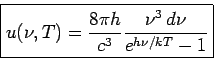
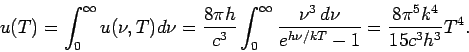
![]() die Energiedichte der Strahlung pro Wellenlängeneinheit,
die Energiedichte der Strahlung pro Wellenlängeneinheit,