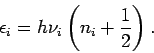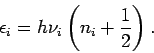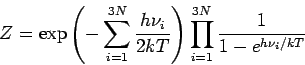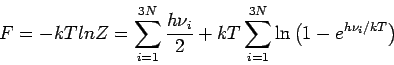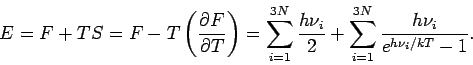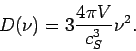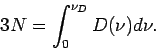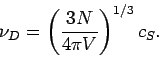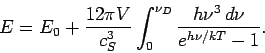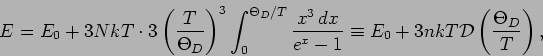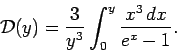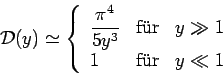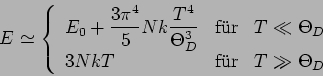Nächste Seite: Systeme Wechselwirkender Teilchen
Aufwärts: Photonen und Phononen
Vorherige Seite: Zustandsgleichung des Photonengases
Das Modell von EINSTEIN zur spezifischen Wärme der Festkörper
hat zu zu kleinen Werten von 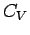 bei tiefen Temperaturen geführt.
Nach DEBYE soll man das Bose-Gas der Phononen
(quantisierte Schallwellen) in Festkörpern als das eigentliche dafür
verantwortliche System betrachten. Es gibt daher nicht die einheitliche
Schwingungsfrequenz
bei tiefen Temperaturen geführt.
Nach DEBYE soll man das Bose-Gas der Phononen
(quantisierte Schallwellen) in Festkörpern als das eigentliche dafür
verantwortliche System betrachten. Es gibt daher nicht die einheitliche
Schwingungsfrequenz 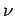 , sondern einen Satz von Schwingungsfrequenzen
, sondern einen Satz von Schwingungsfrequenzen
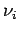 (Eigenfrequenzen der möglichen Schwingungsmoden des Systems aus
(Eigenfrequenzen der möglichen Schwingungsmoden des Systems aus
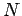 wechselwirkenden Atome). Da es insgesamt
wechselwirkenden Atome). Da es insgesamt 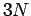 Freiheitsgrade gibt, gibt es
genau
Freiheitsgrade gibt, gibt es
genau 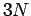 solcher Frequenzen. Für jedem solchen Oszillator gilt:
solcher Frequenzen. Für jedem solchen Oszillator gilt:
In bekannter Weise folgt:
(der erste Multiplikator entspricht den Nullpunktenergien der Oszillatoren).
Daher gilt:
und
Übergang zum Kontinuum: Anregungen sind die Quantisierte Wellen mit linearen
Dispersionsgesetz und dem Wellenvektor
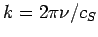 (
(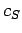 -
Schallgeschwindigkeit in entsprechender Richtung).
-
Schallgeschwindigkeit in entsprechender Richtung).
Im Gegensatz zu Photonen, gibt es hir 3 möglicher Polarizationsrichtungen
(2 transversale und 1 longitudinale Welle). Einfachheitshalber nehmen
wir die Schalgeschwindigkeit in alle diese Richtungen als gleich an. Somit ist die
Zustandsdichte der Phononen
Man beachte dass die Anzahl alle Oszillatoren 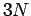 ist. Es existiert deswegen
eine maximale Frequenz der Schwingungen
ist. Es existiert deswegen
eine maximale Frequenz der Schwingungen 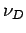 (die DEBYE-Frequenz), so dass
(die DEBYE-Frequenz), so dass
Diese ist dann:
Damit ist die innere Energie
Unter Einfhrung der DEBYE-Temperatur
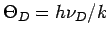 erhält man:
erhält man:
mit der DEBYE-Funktion
Das Grenzwertverhalten der Debye-Fkt.
gibt Aufrschlüsse über thermodynamische Verhalten des Debye-Modells:
und, entsprechend,



Nächste Seite: Systeme Wechselwirkender Teilchen
Aufwärts: Photonen und Phononen
Vorherige Seite: Zustandsgleichung des Photonengases
Prof. Igor Sokolov
2004-07-01