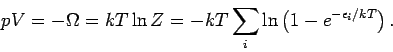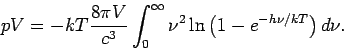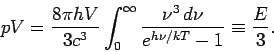Nächste Seite: Phononen: Das Debye-Modell
Aufwärts: Photonen und Phononen
Vorherige Seite: Das Planck'sche Strahlungsgesetz
Bose-Gas mit 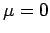

Der Kontinuumsübergang ergibt
Nach der partiellen Integration erhält man:
Bemerkung 1: Die beiden Teile der Gleichung sind proportional zu 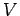 ,
daher hängt der Druck
,
daher hängt der Druck 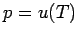 nur von der Temperatur und nicht von dem Volumen ab.
nur von der Temperatur und nicht von dem Volumen ab.
Bemerkung 2: Vgl.: für Bose-Gas aus massiven Teilchen hat man
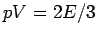 . Das Vorfaktor vor
. Das Vorfaktor vor 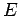 hängt unmittelbar mit der Form des
Dispersionsgesetzes
hängt unmittelbar mit der Form des
Dispersionsgesetzes
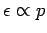 bzw.
bzw.
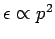 zusammen.
zusammen.
Prof. Igor Sokolov
2004-07-01
![]()
![]()