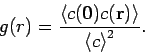Die radiale Paarverteilungsfunktion ![]() ist proportional zur bedingten
Wahrscheinlichkeit, am Abstand
ist proportional zur bedingten
Wahrscheinlichkeit, am Abstand ![]() von einem ausgewählten
Teilchen(-zentrum) einen anderes Teilchen zu finden:
von einem ausgewählten
Teilchen(-zentrum) einen anderes Teilchen zu finden:
![]() .
Normierung der Fkt.
.
Normierung der Fkt. ![]() ist anders als bei der Wahrscheinlichkeit: sie ist
durch die Forderung der Korrelationsentkopplung gegeben:
ist anders als bei der Wahrscheinlichkeit: sie ist
durch die Forderung der Korrelationsentkopplung gegeben:
Bemerkung: Die Funktion ![]() ist, natürlich, vom
Zustand des Systems abhängig, damit ist die Funktion auch von
Temperatur, chemischen Potential, u.s.v. abhängig.
ist, natürlich, vom
Zustand des Systems abhängig, damit ist die Funktion auch von
Temperatur, chemischen Potential, u.s.v. abhängig.
Andere Interpretation: sei ![]() die lokale Teilchendichte, d.h.
eine Wahrscheinlichkeit ein Teilchen (-zentrum) am Punkt
die lokale Teilchendichte, d.h.
eine Wahrscheinlichkeit ein Teilchen (-zentrum) am Punkt ![]() zu
finden. (Bem.:
zu
finden. (Bem.:
![]() ). Dann gilt:
). Dann gilt: