


Nächste Seite: Die Paarverteilungsfunktion und die
Aufwärts: Statistische Theorie dichter Fluide
Vorherige Seite: Die radiale Paarverteilungsfunktion
Die Paarverteilungsfunktion ist eine beobachtbare Größe: Sie kann in
elastischen Streuexperimenten (Neutronen oder Röntgenstrahlung) gemessen
werden.
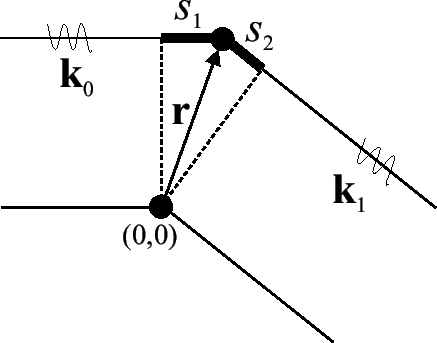
Bei Streuung einer flachen Welle auf einem einzelnen Atom (im Ursprung
der Koordinaten) entsteht eine Kugelwelle mit einer winkelabhängigen
Amplitude:
(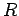 : Abstand vom Detektor,
: Abstand vom Detektor, 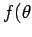 ): Atom- (Molekül-)formfaktor
(Streuamplitude)). Befindet sich ein Atom nicht am Koordinatenursprung, so
entsteht eine Phasendifferenz
): Atom- (Molekül-)formfaktor
(Streuamplitude)). Befindet sich ein Atom nicht am Koordinatenursprung, so
entsteht eine Phasendifferenz
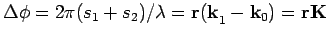 , mit
, mit
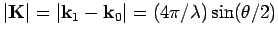 .
.
Die Gesamtamplitude 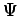 der Streustrahlung am Detektor ist die
Superposition der Beiträge aller Atome:
der Streustrahlung am Detektor ist die
Superposition der Beiträge aller Atome:
(Annahme: Abstand 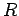 zum Detektor ist groß verglichen mit den typische
Abstände zwischen der streuenden Atome: Alle
zum Detektor ist groß verglichen mit den typische
Abstände zwischen der streuenden Atome: Alle 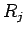 sind gleich). Die
Intensität am Detektor:
sind gleich). Die
Intensität am Detektor:
mit
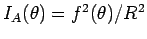 .
. 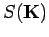 ist der
Strukturfaktor
ist der
Strukturfaktor
(Übergang zu Variablen
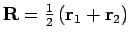 und
und
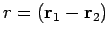 )
) 
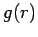 kann aus der Fourier-Transformation der messbaren
Größe
kann aus der Fourier-Transformation der messbaren
Größe 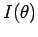 bestimmt werden.
bestimmt werden.
Bemerkung:
Für
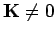 (Übergang zur Kugelkoordinaten)
(Übergang zur Kugelkoordinaten)
Prof. Igor Sokolov
2004-07-01
![]() der Streustrahlung am Detektor ist die
Superposition der Beiträge aller Atome:
der Streustrahlung am Detektor ist die
Superposition der Beiträge aller Atome:
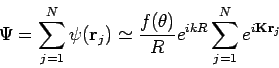
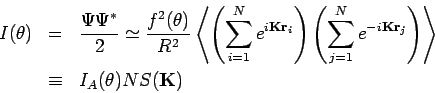
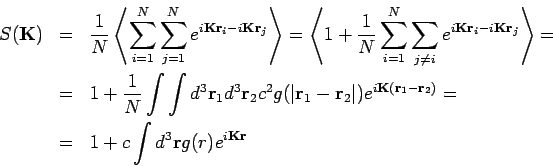
![\begin{eqnarray*}
S(\mathbf{K)} &=&1+c\int \left[ g(r)-1\right] e^{i\mathbf{Kr}}...
...+c\int h(r)e^{i\mathbf{Kr}}d^{3}\mathbf{r}+c\delta (\mathbf{K).}
\end{eqnarray*}](img602.png)