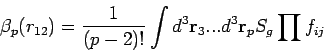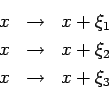Nächste Seite: Phasenübergänge
Aufwärts: Statistische Theorie dichter Fluide
Vorherige Seite: Die BGY-Gleichung
Andere Integralgleichungen der Theorie dichter Fluide können
durch Näherungen für die direkte Korrelationsfunktion
hergeleitet werden (hier nur kurze Besprechung; die detalliertere
Betrachtung siehe BALESCU). Ausgangspunkt dazu ist eine
Ornstein-Zernicke-Gleichung für 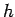 :
:
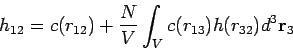 |
(19) |
mit der direkten Korrelationsfunktion 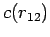 . Das 1. Glied der
Gleichung beschreibt den Beitrag der unmittelbaren Wechselwirkung zwischen
Teilchen 1 und 2, das 2. Glied - die Beiträge aller anderen Teilchen. Es
gibt verschiede Anzätze, die die Näherungen für
. Das 1. Glied der
Gleichung beschreibt den Beitrag der unmittelbaren Wechselwirkung zwischen
Teilchen 1 und 2, das 2. Glied - die Beiträge aller anderen Teilchen. Es
gibt verschiede Anzätze, die die Näherungen für 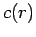 liefern.
Zum Beispiel, kann man annehmen, dass das Potential mittlerer Kraft
liefern.
Zum Beispiel, kann man annehmen, dass das Potential mittlerer Kraft
so dass
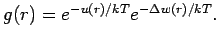 Bez.:
Bez.:
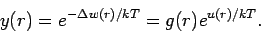 |
(20) |
Die Annahme
in Gl.(19) eingesetzt, führt zu einer geschlossenen Gleichung für 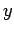 :
:
(PERKUS + YEVICK, 1958). Die PY-Gleichung ist für ein
Gas harter Kugeln exakt lösbar. Die Zustandsgleichungen sind:
Aus der Druckgleichung folgt
aus Kompressibilitätsgleichung folgt
wobei
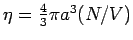 ist die dimensionslose Dichte des
Gases. Der Unterschied zwischen 2 Formen der Zustandsgleichung ist nicht
groß und charakterisiert die Qualität der Näherung. Die andere
bekannte Integralgleichung ist die sog. HNC-Gleichung (Hypernetterd Chains),
RUSHBROOKE, 1960. Die Gleichung geht effektiv von der Annahme aus
ist die dimensionslose Dichte des
Gases. Der Unterschied zwischen 2 Formen der Zustandsgleichung ist nicht
groß und charakterisiert die Qualität der Näherung. Die andere
bekannte Integralgleichung ist die sog. HNC-Gleichung (Hypernetterd Chains),
RUSHBROOKE, 1960. Die Gleichung geht effektiv von der Annahme aus
(vgl. mit der Taylorentwicklung von Gl.(20). Die entsprechende
Integralgleichung lautet:
Für ein Gas harter Kugeln liefert diese Gleichung etwas schlechtere
Ergebnisse, als PY.
Bemerkung 1: Die Paarverteilungsfunktion erlaubt eine
Virialentwicklung in der Form
mit
wobei 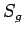 ein entsprechender kombinatorischer Faktor ist. Die Diagramme,
die die Clusterintegrale für
ein entsprechender kombinatorischer Faktor ist. Die Diagramme,
die die Clusterintegrale für 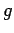 repräsentieren, unterscheiden
sich von denjenigen in der Mayer-Entwicklung durch Festhalten der
Positionen der
Teilchen 1 und 2, über deren Koordinaten nicht integriert wird.
repräsentieren, unterscheiden
sich von denjenigen in der Mayer-Entwicklung durch Festhalten der
Positionen der
Teilchen 1 und 2, über deren Koordinaten nicht integriert wird.
Für die oben diskutierten Integralgleichungen kann festgestellt werden,
welche Diagramme dabei berücksichtigt worden sind. Interessanterweise
subsummiert die HNC-Gleichung mehr Diagrammenklassen als PY. Mehr ist also
nicht immer besser!
Bemerkung 2. Fast die gesamte Information über
das Verhalten von Fluiden wird aus numerischer Simulationen gewonnen.
Diese macht man entweder mikrokanonisch (Methode der Molekulardynamik),
indem man die Bewegungsgleichungen eines mittelgroßen Teilchensystems
numerisch löst, oder kanonisch, mittels der Monte-Carlo-Methode. Dabei
wird die richtige Dynamik des Systems durch ein ''Spiel'' ersetzt. Jeder
Monte-Carlo Schritt (''Zug'') besteht aus der Veränderung der
Koordinaten eines Teilchens
wobei 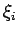 Zufallszahlen sind. Es wird die potenzielle Energie des
Systems
Zufallszahlen sind. Es wird die potenzielle Energie des
Systems
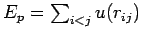 bestimmt. Wenn diese Energie nach einem
Schritt kleiner ist, als vor dem Schritt, wird dieser Schritt mit der
Wahrscheinlichkeit 1 angenommen. Wenn dagegen die potenzielle Energie sich
um den Wert
bestimmt. Wenn diese Energie nach einem
Schritt kleiner ist, als vor dem Schritt, wird dieser Schritt mit der
Wahrscheinlichkeit 1 angenommen. Wenn dagegen die potenzielle Energie sich
um den Wert 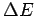 erhöht, wird der Schritt nur mit der
Wahrscheinlichkeit
erhöht, wird der Schritt nur mit der
Wahrscheinlichkeit
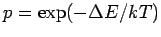 angenommen. Diese Regel (METROPOLIS-Algorithmus) führt zu einem Gleichgewichtszustand, in dem
die Wahrscheinlichkeiten der entsprechenden Mikrozustände durch die
Boltzmann-Faktoren gegeben sind:
angenommen. Diese Regel (METROPOLIS-Algorithmus) führt zu einem Gleichgewichtszustand, in dem
die Wahrscheinlichkeiten der entsprechenden Mikrozustände durch die
Boltzmann-Faktoren gegeben sind:
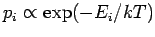 . Nach
. Nach 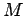 Schritten werden die Mittelwerte der dynamischen Variablen oder der
Verteilungsfunktionen bestimmt.
Schritten werden die Mittelwerte der dynamischen Variablen oder der
Verteilungsfunktionen bestimmt.



Nächste Seite: Phasenübergänge
Aufwärts: Statistische Theorie dichter Fluide
Vorherige Seite: Die BGY-Gleichung
Prof. Igor Sokolov
2004-07-01
![]() :
:
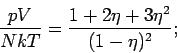
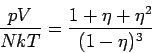
![\begin{displaymath}
g(r)=e^{-u(r)/kT}\left[ 1+\sum_{p=3}^{\infty }\beta _{p}(r)\left( \frac{N}{V}%
\right) ^{p-2}\right]
\end{displaymath}](img702.png)