


Nächste Seite: Andere Integralgleichungen.
Aufwärts: Statistische Theorie dichter Fluide
Vorherige Seite: Verallgemeinerte Verteilungsfunktionen.
Brauchbare Näherungen bekommt man nur, wenn man diese unendliche
Kette der Gleichungen an irgendeinem Schritt abbricht. Da thermodynamische
Größen von der Paarverteilungsfunktion
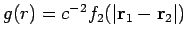 abhängig sind, empfiehlt sich als
einfachste Näherung die Entkopplung auf dem Niveau der 2. Gleichung der
Hierarche. Schreiben wir die Gl.(18) für
abhängig sind, empfiehlt sich als
einfachste Näherung die Entkopplung auf dem Niveau der 2. Gleichung der
Hierarche. Schreiben wir die Gl.(18) für 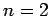 : und dividieren
beide Teile durch
: und dividieren
beide Teile durch
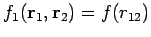 . Wir
erhalten
. Wir
erhalten
Hier liefert
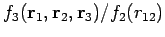 die bedingte Wahrscheinlichkeit das Teilchen 3 im Punkt
die bedingte Wahrscheinlichkeit das Teilchen 3 im Punkt
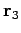 zu finden, vorausgesetzt, die Teilchen 1 und 2 sitzen in
zu finden, vorausgesetzt, die Teilchen 1 und 2 sitzen in
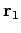 und
und
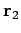 , so dass die rechte Seite der Gleichung
nicht anders ist, als die mittlere Kraft, das auf das Teilchen 1 in
Anwesenheit von Teilchen 2 und 3 wirkt, so dass
, so dass die rechte Seite der Gleichung
nicht anders ist, als die mittlere Kraft, das auf das Teilchen 1 in
Anwesenheit von Teilchen 2 und 3 wirkt, so dass
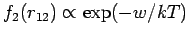 , wobei
, wobei 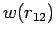 das Potential dieses mittleren Krafts ist. Es
ist bequem, von der Funktion
das Potential dieses mittleren Krafts ist. Es
ist bequem, von der Funktion
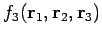 zu einer dimensionslosen 3-Teilchen Verteilungsfunktion
überzugehen,
zu einer dimensionslosen 3-Teilchen Verteilungsfunktion
überzugehen,
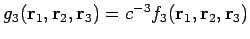 .
Für
.
Für
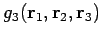 empfiehlt sich eine sog. KIRKWOOD-Näherung (1935):
empfiehlt sich eine sog. KIRKWOOD-Näherung (1935):
Unter diese Annahme bekommen wir eine geschlossene
Integrodifferentialgleichung für 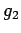 , die BORN-GREEN-YVON-Gleichung (BGY):
, die BORN-GREEN-YVON-Gleichung (BGY):
Prof. Igor Sokolov
2004-07-01
![]() abhängig sind, empfiehlt sich als
einfachste Näherung die Entkopplung auf dem Niveau der 2. Gleichung der
Hierarche. Schreiben wir die Gl.(18) für
abhängig sind, empfiehlt sich als
einfachste Näherung die Entkopplung auf dem Niveau der 2. Gleichung der
Hierarche. Schreiben wir die Gl.(18) für ![]() : und dividieren
beide Teile durch
: und dividieren
beide Teile durch
![]() . Wir
erhalten
. Wir
erhalten
![\begin{displaymath}
-kT\nabla _{1}\left[ \ln f_{2}(r_{12})\right] =\nabla _{1}u_...
...mathbf{r}_{1}\mathbf{r}_{2},%
\mathbf{r}_{3})}{f_{2}(r_{12})}.
\end{displaymath}](img675.png)