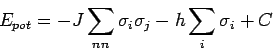a) Binäre Legierung, z.B. Cu![]() Zn
Zn![]() . Hier ist
. Hier ist ![]() wenn der Gitterplatz
wenn der Gitterplatz ![]() durch einen Cu-Atom und
durch einen Cu-Atom und
![]() wenn der Platz durch den Zn-Arom besetzt wird. Der Beitrag
kinetischer Freiheitsgrade entkoppelt. Die Potentielle Energie lautet:
wenn der Platz durch den Zn-Arom besetzt wird. Der Beitrag
kinetischer Freiheitsgrade entkoppelt. Die Potentielle Energie lautet:
![\begin{eqnarray*}
E_{pot} &=& \frac{1}{4}\sum_{nn}J_{CuCu}(1+\sigma _{i})(1+\sig...
...gma _{i})(1-\sigma
_{j})+(1-\sigma _{j})(1+\sigma _{j})\right] .
\end{eqnarray*}](img740.png)
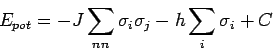
b) Das Gittergas. Jedem platz auf einem Gitter wird eine Variable ![]() gegenübergestellt. Wenn dieser Platz als besetzt gilt, dann ist
gegenübergestellt. Wenn dieser Platz als besetzt gilt, dann ist ![]() , wenn der Platz leer ist, dann ist
, wenn der Platz leer ist, dann ist ![]() . In diesem Fall ist
. In diesem Fall ist
![]() . Die Einführing der Variable
. Die Einführing der Variable
![]() reduziert das Modell zu einem Ising-Modell. Man hat:
reduziert das Modell zu einem Ising-Modell. Man hat: