Korrespondenz zwischen Gitter-Gas und Ising-Modellen

Der Hauptunterschied zwischen den Gitter-Gas und Ising-Modellen liegt in der Tatsache, dass die Gesamtzahl der Teilchen eines Gittergases konstant bleibt, wobei der Gesamspin eines Spinsystems sich ändern kann.

Für das Gittergas gibt daher eine Nebenbedingung $\sum_{i}t_{i}=n$, wobei $n$ die Gesamtzahl der Teilchen ist, d.h. $\sum_{i}\sigma _{i}=2n-N$.

Kanonische Zustandssumme (Räumlicher Anteil)

$$Z=\sum_{\sum p_i = n} \exp \left( -\beta E_ {pot} \right)$$

Die großkanonische Zustandssumme

$$Z_G = \sum_{n=0}^\infty \exp(\beta \mu n) \sum_{\sum p_i = n} \exp \left( -\beta E_ {pot} \right)$$

$$= \sum_{\mbox{all} \atop \mbox{configurations} } \exp \left(-\beta E_ {pot} - \mu \sum_i p_i \right)$$

$$= \sum_{\mbox{all} \atop \mbox{configurations} } \exp \left(-\beta E_{pot} - \mu n \right).$$

entspricht einer Kanonischen Zustandssumme eines Ising-Modells. Die kinetischen Eigenschaften der Modelle unterscheiden sich bei gleicher Thermodynamik.

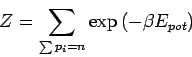
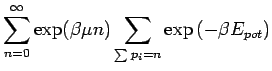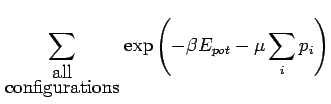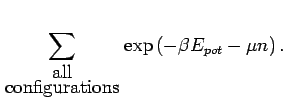Die nicht-konservative Glauber-Dynamik normaler Ising-Modell erlaubt das Kippen des Einzelspins, die konservative Kawasaki-Dynamik, dass z.B. dem Austausch von einem Besetztem und einem leeren Platz bei der Teilchenbewegung in einem Gittergasmodell entspricht, erlaubt nur das Austauschen der Ausrichtungen zweier benachbarnten Spins.

$$\uparrow \uparrow \Downarrow \downarrow \uparrow \quad \rightarrow \quad \uparrow \uparrow \Uparrow \downarrow \uparrow$$

Glauber-Dynamik

$$\uparrow \Uparrow \Downarrow \downarrow \uparrow \quad \rightarrow \quad \uparrow \Downarrow \Uparrow \downarrow \uparrow$$

Kawasaki-Dynamik

($\Uparrow$ - zu rotierende Spins).