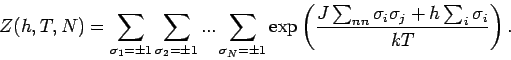
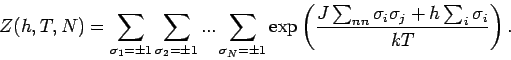
Aus ![]() folgen alle thermodynamische Funktionen. Von Interesse sind:
folgen alle thermodynamische Funktionen. Von Interesse sind:
![]() Das Potential
Das Potential
![]() (''freie
Enthalpie für Magnetika''). Dieses wird oft als die ''freie
Energie'' bezeichnet, obwohl die richtige freie Energie eigentlich die
Funktion von einer extensiven Variable
(''freie
Enthalpie für Magnetika''). Dieses wird oft als die ''freie
Energie'' bezeichnet, obwohl die richtige freie Energie eigentlich die
Funktion von einer extensiven Variable ![]() sein sollte. Solche richtige Form,
sein sollte. Solche richtige Form,
![]() wird z.B. in der Landau-Theorie vorausgesetzt. Das gleiche
gilt auch für die entsprechende innere Energie.
wird z.B. in der Landau-Theorie vorausgesetzt. Das gleiche
gilt auch für die entsprechende innere Energie.
![]() Innere Energie
Innere Energie
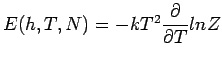
![]() Spezifische Wärme
Spezifische Wärme
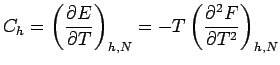
![]() Magnetisierung
Magnetisierung
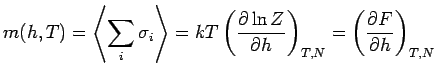
Ziel: Exakte oder näherungsweise Bestimmung von ![]() .
.