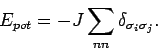
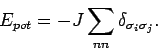
![]() Die eindimensionale Systeme können i.d.R. exakt betrachtet werden.
Die eindimensionale Systeme können i.d.R. exakt betrachtet werden.
![]() Für einige zweidimensionale Modelle sind die exakten geschlossenen Ausdrücke
für der Zustandsummen bekannt. Die erste Lösung war die exakte Zustandssumme für 2-dimensionale
Ising Modell, ONSAGER, 1944.
Für einige zweidimensionale Modelle sind die exakten geschlossenen Ausdrücke
für der Zustandsummen bekannt. Die erste Lösung war die exakte Zustandssumme für 2-dimensionale
Ising Modell, ONSAGER, 1944.
![]() Die dreidimensional Situation hat bis jetzt zu keiner geschlossenen Form geführt.
Die dreidimensional Situation hat bis jetzt zu keiner geschlossenen Form geführt.
![]() Die unendlichdimensionale Gitter (Vollständige Graphen oder Bäume) erlauben
i.d.R. exakte Betrachtung.
Die unendlichdimensionale Gitter (Vollständige Graphen oder Bäume) erlauben
i.d.R. exakte Betrachtung.