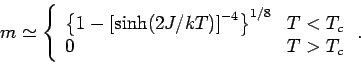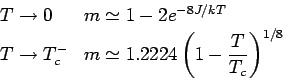Nächste Seite: Moderne Theorie der Phasenübergänge
Aufwärts: Ising-Modell und verwandte Gittermodelle.
Vorherige Seite: Die Korrelationslänge
Hier geben wir nur eine Übersicht der Resultaten. Die Exakte Lösung für
die Zustandssumme ohne Feld: ONSAGER, 1944. Vereinfachungen:
NEWELL and MONTROLL (1953), DOMB (1960),
HUAN (1963), SCHULTZ, MATTIS und LIEB
(1964), und viele andere. Die wesentliche Vereinfachung: VDOVICHENKO
(1964). Das Zugang basiert auf der Methode der unsere vorherige Ausführung
recht ähnlich ist (Siehe Nolting, º 4.4).
Ergebnis:
Folgerungen:
(Vgl: MFA
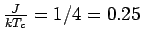 , Bethe
, Bethe
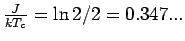 ).
Die exakte Übergangstemperatur ist kleiner als die von der Näherungen gegebene.
Die innere Energie und die spezifische Wärme lassen sich analytisch durch elliptische Integrale ausdrucken. In der Nähe von
).
Die exakte Übergangstemperatur ist kleiner als die von der Näherungen gegebene.
Die innere Energie und die spezifische Wärme lassen sich analytisch durch elliptische Integrale ausdrucken. In der Nähe von 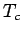 ist
ist
so dass
d.h. die spezifische Wärme divergiert logarithmisch am 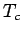 (vgl. mit einem endlichen Sprung
bei der MF oder Bethe Näherungen).
(vgl. mit einem endlichen Sprung
bei der MF oder Bethe Näherungen).
Spontane Magnetisierung. Hier ist die Lösung für 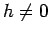 benötigt.
(Die Lösung wurde von Onsager 1949 angekündigt, ist aber nie publiziert worden.) Die erste
publizierte Lösung stammt von YANG (1952).
Im Grenzfall
benötigt.
(Die Lösung wurde von Onsager 1949 angekündigt, ist aber nie publiziert worden.) Die erste
publizierte Lösung stammt von YANG (1952).
Im Grenzfall
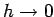 hat man
hat man
Spezialfälle:
Der entsprechende kritische Exponent 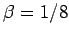 ist kleiner als in
der MF. Das Phasenübergang wirkt
sich im Ordnungsparameter sehr ausgeprgt aus, die Näherungen weichen diesen Effekt auf.
ist kleiner als in
der MF. Das Phasenübergang wirkt
sich im Ordnungsparameter sehr ausgeprgt aus, die Näherungen weichen diesen Effekt auf.



Nächste Seite: Moderne Theorie der Phasenübergänge
Aufwärts: Ising-Modell und verwandte Gittermodelle.
Vorherige Seite: Die Korrelationslänge
Prof. Igor Sokolov
2004-07-01
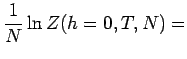
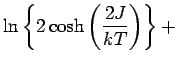
![$\displaystyle \frac{1}{2 \pi} \int_0^\pi d \phi \ln \left[
\frac{1}{2} + \frac{1}{2} \sqrt{1 - \frac{2 \sinh(2J/kT)}{\cosh^2(2J/kT)}
\sin^2 \phi} \right] .$](img925.png)
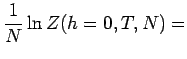
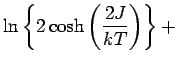
![$\displaystyle \frac{1}{2 \pi} \int_0^\pi d \phi \ln \left[
\frac{1}{2} + \frac{1}{2} \sqrt{1 - \frac{2 \sinh(2J/kT)}{\cosh^2(2J/kT)}
\sin^2 \phi} \right] .$](img925.png)
![\begin{displaymath}
C_{h=0}(T)=\frac{8Nk}{\pi} \left( \frac{J}{kT_c} \right)^2
\...
... \ln \left( \frac{2kT_c}{J} \right) - 1-\frac{\pi}{4} \right],
\end{displaymath}](img929.png)
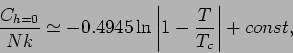
![]() benötigt.
(Die Lösung wurde von Onsager 1949 angekündigt, ist aber nie publiziert worden.) Die erste
publizierte Lösung stammt von YANG (1952).
Im Grenzfall
benötigt.
(Die Lösung wurde von Onsager 1949 angekündigt, ist aber nie publiziert worden.) Die erste
publizierte Lösung stammt von YANG (1952).
Im Grenzfall
![]() hat man
hat man