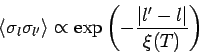Nächste Seite: Resultate für das Ising-Modell
Aufwärts: Das Ising-Modell in einer
Vorherige Seite: Das Ising-Modell in einer
Berechnen wir für 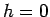 die Wahrscheinlichkeit
die Wahrscheinlichkeit  , dass Spins
, dass Spins  und
und
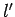 gleichgerichtet sind (
gleichgerichtet sind (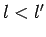 ). Diese Wahrscheinlichkeit ist mit der
Korrelationsfunktion
). Diese Wahrscheinlichkeit ist mit der
Korrelationsfunktion
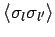 verbunden:
verbunden:
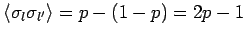 . Berechnung von
. Berechnung von
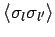 :
:
mit
Für 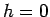 hat die Matrix
hat die Matrix 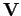 die Eigenwerte
die Eigenwerte
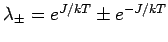 und die Eigenvektoren
und die Eigenvektoren
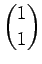 und
und
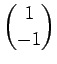 . In der Diagonaldarstellung von
. In der Diagonaldarstellung von  ist
ist
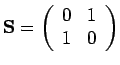 . Damit ist
. Damit ist
Da
bekommt man
Für 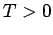 nimmt
nimmt
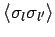 exponentiell mit dem
Abstand
exponentiell mit dem
Abstand 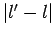 ab:
ab:
Die Korrelationslänge
![$\xi(T)= \ln [ \tanh(J/kT)] $](img922.png) (Reichweite der Ordnung) divergiert für
(Reichweite der Ordnung) divergiert für
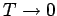 .
.
Prof. Igor Sokolov
2004-07-01
![$\displaystyle Z^{-1} Sp \left[ \mathbf{V}^l \mathbf{S} \mathbf{V}^{l'-l} \mathbf{S}
\mathbf{V}^{N-l'} \right],$](img911.png)
![$\displaystyle Z^{-1} Sp \left[ \mathbf{V}^l \mathbf{S} \mathbf{V}^{l'-l} \mathbf{S}
\mathbf{V}^{N-l'} \right],$](img911.png)
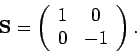
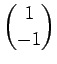 . In der Diagonaldarstellung von
. In der Diagonaldarstellung von 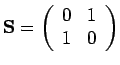 . Damit ist
. Damit ist
![\begin{displaymath}
\left \langle \sigma_l \sigma_{l'} \right \rangle =
Z^{-1} S...
...N-l'} & 0 \\ 0 & \lambda_-^{N-l'}
\end{array}\right)
\right].
\end{displaymath}](img917.png)
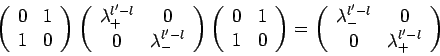
![\begin{displaymath}
\left \langle \sigma_l \sigma_{l'} \right \rangle =
\frac{\l...
...} =
\left[ \tanh \left( \frac{J}{kT} \right) \right]^{l'-l}.
\end{displaymath}](img919.png)