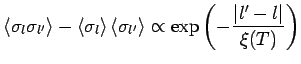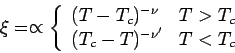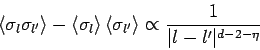Nächste Seite: Universalitätshypothese
Aufwärts: Moderne Theorie der Phasenübergänge
Vorherige Seite: Moderne Theorie der Phasenübergänge
Nahe am Phasenübergang zeigen viele thermodynamische Größen Potenz-artiges Verhalten.
So gilt:
 Für die spezifische Wärme
Für die spezifische Wärme
(Dem endlichen Sprung / logarithmische Divergenz entsprechen
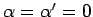 )
)
 Für die Magnetisierung (Dichte in Gittegas / Legirung - Modelle)
Für die Magnetisierung (Dichte in Gittegas / Legirung - Modelle)
 Für die Suszeptibilität (Kompressibilität)
Für die Suszeptibilität (Kompressibilität)
 Kritische Isotherme: Da
Kritische Isotherme: Da 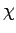 für
für 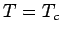 divergiert, gilt
divergiert, gilt
mit 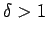 (für Gase
(für Gase
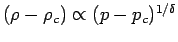 ).
).
 Für die Korrelationslänge (bestimmt durch
Für die Korrelationslänge (bestimmt durch
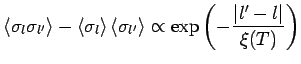
Für 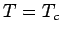 divergiert
divergiert 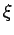 . In diesem Fall gilt
. In diesem Fall gilt
(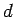 - Raumdimension).
- Raumdimension).
Die wichtigsten kritischen Exponenten:
Prof. Igor Sokolov
2004-07-01
![]() Für die spezifische Wärme
Für die spezifische Wärme
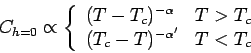
![]() Für die Magnetisierung (Dichte in Gittegas / Legirung - Modelle)
Für die Magnetisierung (Dichte in Gittegas / Legirung - Modelle)
![]() Für die Suszeptibilität (Kompressibilität)
Für die Suszeptibilität (Kompressibilität)
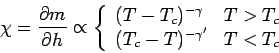
![]() Für die Korrelationslänge (bestimmt durch
Für die Korrelationslänge (bestimmt durch