


Nächste Seite: Die Skalenhypothese
Aufwärts: Moderne Theorie der Phasenübergänge
Vorherige Seite: Kritische Exponenten
GRIFFITHS, 1970. Die kritische Exponenten sind universal, d.h. sie
hängen nur von den folgenden Eigenscheften des System ab:
Für die Wechselwirkungspotentiale
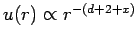 (z.B. in einem Gas) mit
(z.B. in einem Gas) mit 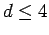 unterscheidet man die folgende Situationen:
unterscheidet man die folgende Situationen:

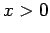 - kurzreichweitige Wechselwirkung
- kurzreichweitige Wechselwirkung

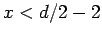 - sehr reichweitige Wechselwirkung (in diesem Fall
liefert die MF-Theorie die richtige Werte der kritischen Exponenten)
- sehr reichweitige Wechselwirkung (in diesem Fall
liefert die MF-Theorie die richtige Werte der kritischen Exponenten)

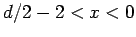 - nichtuniversaler Bereich der mittelreichweitigen
WW: Kritische Exponenten sind von
- nichtuniversaler Bereich der mittelreichweitigen
WW: Kritische Exponenten sind von 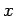 explizit abhängig.
explizit abhängig.
Aus der Thermodynamik kennen wir die folgende Ungleichungen für die
kritische exponenten
Für exakt lösbare Modelle (Ising und andere) und die meisten experimentellen Daten
(innerhalb der Fehlergrenzen)
liegen diese Ungleichungen stets als Identitäten vor. Die Exponenten an beiden Seiten des
Übergangs (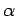 und
und 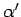 ,
, 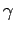 und
und 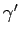 usw.) sind stets gleich.
usw.) sind stets gleich.
Interessant: Für das MF-Resultat des Ising-Modell (sog. klassische Exponenten)
sind die Gl.(1)-(5) erfüllt.
Unter der Annahme, das die Gl.(6) und (7) die räumliche Dimension eines MF-systems definieren,
bekommen wir: Aus (6) bekommt man
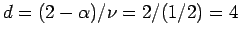 , aus (7)
, aus (7)
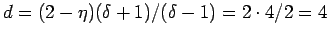 .
. 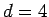 ist die obere kritische Dimension für das
Ising-Modell.
ist die obere kritische Dimension für das
Ising-Modell.



Nächste Seite: Die Skalenhypothese
Aufwärts: Moderne Theorie der Phasenübergänge
Vorherige Seite: Kritische Exponenten
Prof. Igor Sokolov
2004-07-01
![]()
![]() - kurzreichweitige Wechselwirkung
- kurzreichweitige Wechselwirkung
![]()
![]() - sehr reichweitige Wechselwirkung (in diesem Fall
liefert die MF-Theorie die richtige Werte der kritischen Exponenten)
- sehr reichweitige Wechselwirkung (in diesem Fall
liefert die MF-Theorie die richtige Werte der kritischen Exponenten)
![]()
![]() - nichtuniversaler Bereich der mittelreichweitigen
WW: Kritische Exponenten sind von
- nichtuniversaler Bereich der mittelreichweitigen
WW: Kritische Exponenten sind von ![]() explizit abhängig.
explizit abhängig.

![]() , aus (7)
, aus (7)
![]() .
. ![]() ist die obere kritische Dimension für das
Ising-Modell.
ist die obere kritische Dimension für das
Ising-Modell.