Der Dezimierungsvorgang entspricht im einfachsten Fall dem Aufsummieren über
die Ausrichtungen jedes zweiten Spins. Die Gitterplätze eines
quadratischen Gitters werden durch die Paare ![]() natürlicher Zahlen
numeriert. Die Spins mit
natürlicher Zahlen
numeriert. Die Spins mit ![]() gerade werden als
gerade werden als ![]() bezeichnet (diese
werden eliminiert) und die Spins mit
bezeichnet (diese
werden eliminiert) und die Spins mit ![]() ungerade werden als
ungerade werden als ![]() bezeichent (diese bleiben). Wir betrachten der Situation mit
bezeichent (diese bleiben). Wir betrachten der Situation mit ![]() , aber mit
''diagonalen'' WW zwischen den übernächsten Nachbarn. Die Zustandssumme
lautet
, aber mit
''diagonalen'' WW zwischen den übernächsten Nachbarn. Die Zustandssumme
lautet
![]() mit
mit
![]() .
.

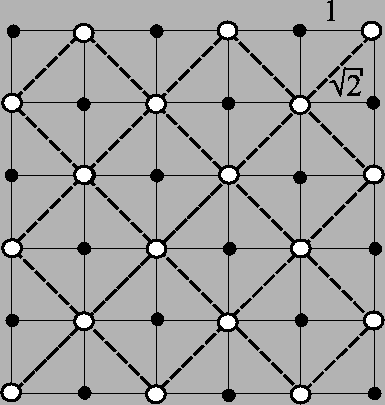
1. Schritt: Renormierund der ''Hamiltonfunktion''.
Die Wahrscheinlichkeiten der Spinskofigurationen in Ausgangssystem ist
![\begin{displaymath}
Z^{(n)}=\sum_{\sigma_i^{(n)}} \exp[-\mathcal{H}\{\sigma_i^{(n)}\}].
\end{displaymath}](img1074.png)
Man hat:

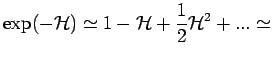 |
|||
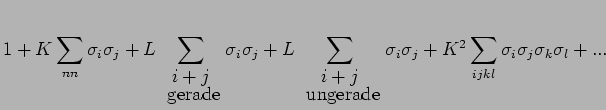 |
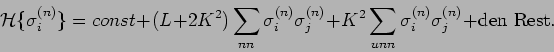
2. Schritt: Renormierung des Parametervektors.
Wir sehen das die 2 Konstanten ![]() , die die Hamiltonfkt. definieren
wie folgt transformiert werden:
, die die Hamiltonfkt. definieren
wie folgt transformiert werden:
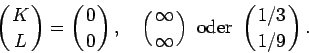
3. Schritt: Linearisierung von R.
Nahe am Fixpunkt
![]() hat man
hat man
![]() mit
mit
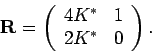
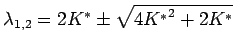 , i.e.
, i.e.
4. Schritt: Berechnung von ![]() .
.
Bei der wiederhohlten Skalentransformation wird der Ausgangspunkt in einer
Folge von Punkten ![]() abgebildet. Das allgemeine Verhalten dieser
Folge hängt von der Position des Anfangpunkts auf der
abgebildet. Das allgemeine Verhalten dieser
Folge hängt von der Position des Anfangpunkts auf der ![]() -Ebene ab.
Betrachten wir das Flußdiagramm der Transformation, siehe Bild.
-Ebene ab.
Betrachten wir das Flußdiagramm der Transformation, siehe Bild.
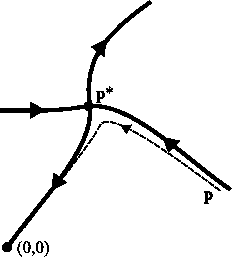
Für typische Werte der Anfangsparameter werden nach mehreren Iterationen
die Punkte
![]() entweder an den stabilen Fixpunkt (0,0) angezogen (
entweder an den stabilen Fixpunkt (0,0) angezogen (![]() , Paramagnet)
oder entfernen sich zu immer größeren Werten von
, Paramagnet)
oder entfernen sich zu immer größeren Werten von ![]() und
und ![]() (Ferromagnet). Es gibt aber die Menge der Anfangspunkten (eine Linie auf
der
(Ferromagnet). Es gibt aber die Menge der Anfangspunkten (eine Linie auf
der ![]() -Fläche), so dass nach mehreren Iterationen der Punkt
-Fläche), so dass nach mehreren Iterationen der Punkt ![]() immer näher an
immer näher an ![]() kommt. Diese Linie entspricht
kommt. Diese Linie entspricht ![]() .
Bei jeder anderen Anfangsbedingung mit
.
Bei jeder anderen Anfangsbedingung mit ![]() nahe am
nahe am ![]() wird sich die Folge
der Abbildungen
wird sich die Folge
der Abbildungen
![]() des Punktes im Parameterraum zuerst
dem Punkt
des Punktes im Parameterraum zuerst
dem Punkt ![]() annähern, und dann, nach Erreichen eines
Umkehtpunktes von ihm immer weiter abweichen. Diese Abweichung wird durch
den positiven Eigenwert
annähern, und dann, nach Erreichen eines
Umkehtpunktes von ihm immer weiter abweichen. Diese Abweichung wird durch
den positiven Eigenwert ![]() beschrieben.
Da
beschrieben.
Da
![]() in der 1. Ordnung von der Größenordnung von
in der 1. Ordnung von der Größenordnung von ![]() ist,
ist,
![]() , sehen wir, dass nach mehreren
Iterationen
, sehen wir, dass nach mehreren
Iterationen
![]() wird. Dies
wird bemerkbar, wenn
wird. Dies
wird bemerkbar, wenn
![]() : Der Vektor
: Der Vektor ![]() tendiert dann gegen die Werte der Parameter, die typisch für para- oder
ferromagnetischen Bereichen sind.
tendiert dann gegen die Werte der Parameter, die typisch für para- oder
ferromagnetischen Bereichen sind.
Anderseits entspricht jeder Schritt der Kadanoff-Transformation
der Verkleinerung der Korrelationslänge um Faktor ![]() , so dass
, so dass
![]() . Wenn
. Wenn
![]() bedeutet das, dass die
neue Blockspins entweder völlig unkorreliert (im paramagnetischen
Bereich) oder völlig korreliert (in ferromagnetischen Bereich) sind.
bedeutet das, dass die
neue Blockspins entweder völlig unkorreliert (im paramagnetischen
Bereich) oder völlig korreliert (in ferromagnetischen Bereich) sind.
Eliminierung von ![]() aus dem System mittels der Beziehungen
aus dem System mittels der Beziehungen
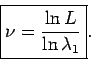
![\begin{displaymath}
\nu=\displaystyle \frac{\ln \sqrt 2}{\ln \left[(2+\sqrt{10})/3 \right]}
\approx 0.65.
\end{displaymath}](img1123.png)
Mit einigen Schwierigkeiten kann man auch die anderen Exponenten bestimmen.