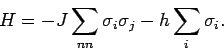
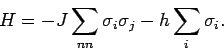
Da für
![]() die Korrelationslänge divergiert,
die Korrelationslänge divergiert,
![]() , kann
, kann ![]() stets so
gewählt werden, dass
stets so
gewählt werden, dass
![]() ist. In einem Cluster, der
vorwiegend aus gleich orientierten Spins besteht,
befinden sich viele Blocks.
ist. In einem Cluster, der
vorwiegend aus gleich orientierten Spins besteht,
befinden sich viele Blocks.
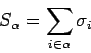
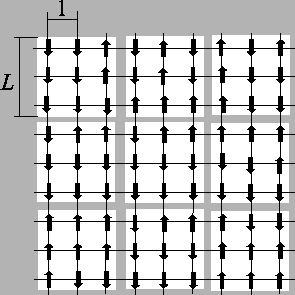
Vergröberung: In der Nähe von ![]() kann man sich das System
in der gleiche Weise aus Cluster korrelierter Blockspins zusammengesetzt
denken, wie aus Cluster der Einzehlspins. D.h.
kann man sich das System
in der gleiche Weise aus Cluster korrelierter Blockspins zusammengesetzt
denken, wie aus Cluster der Einzehlspins. D.h. ![]() kann auch durch die
Blochspins ausgedruckt werden:
kann auch durch die
Blochspins ausgedruckt werden:
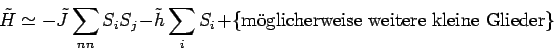
Im kritischen Bereich müssen die freie Energie pro Spin ![]() und die
freie Energie pro Blockspin
und die
freie Energie pro Blockspin
![]() die gleiche
funktionale Gestalt haben, d.h.
die gleiche
funktionale Gestalt haben, d.h.
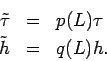
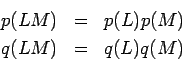
Die Kadanoff-Transformation ![]() lässt die Korrelationslänge
lässt die Korrelationslänge ![]() sich um den Faktor
sich um den Faktor ![]() verkleinern:
verkleinern:
Die Hauptidee der Kadanoff-Transformation ist in verschiedenen Varianten des Renormierungsgruppenzugang realisiert worden:
Die verschiedene Varianten von RSRG (Real space renormalization group) benutzen entweder Mittlung (wie bei Kadanoff), oder die Majoritätsregel (der Blockspin nimmt den Wert an, den die meisten Spins innerhalb des Blocks haben) oder die Dezimierung (den Wert des Blockspins ist mit dem Wert irgendeines Spins des Blocks gleichgesetzt.
Das Verfahren im Fourier-Raum (Wilson RG) benutzt Glättung (Integration
über die höheren Fourier-Komponenten) statt Mittlung.
Diese Transformation wird durch einen Operator ![]() beschrieben:
beschrieben:
Annahme:
![]() . Der invariante
''Hamiltonian'' ist ein Fixpunkt der Transformation
. Der invariante
''Hamiltonian'' ist ein Fixpunkt der Transformation ![]() :
: ![]() .
Da im kritischen Punkt
.
Da im kritischen Punkt
![]() und somit die Eigenschaften
des Systems nicht von
und somit die Eigenschaften
des Systems nicht von ![]() abhängen, entspricht
abhängen, entspricht ![]() genau dem kritischen Punkt.
Die freie Energie
genau dem kritischen Punkt.
Die freie Energie ![]() als Funktional von
als Funktional von ![]() hängt von einem Vektor dem
Parameter
hängt von einem Vektor dem
Parameter ![]() ab.
Z.B. ist für das Ising-Modell
ab.
Z.B. ist für das Ising-Modell
![]() .
. ![]() transformiert diesen
Vektor unter den Skalentransformation (diese Transformation ist nicht unbedingt
linear!):
transformiert diesen
Vektor unter den Skalentransformation (diese Transformation ist nicht unbedingt
linear!):
![]() . Der Vektor
. Der Vektor ![]() entspricht dem Fixpunkt.
entspricht dem Fixpunkt.
Linearisierung nahe des Fixpunktes:
![]() ,
,
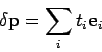
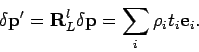
Typischer Weise ist die ganze Prozedur technisch kompliziert. Die beste Literaturquelle zum Weiterlesen ist:
J.J. Binney, N.J. Dowrick, A.J. Fisher and M.E.J. Newman, The Theory of critical Phenomena, Clarendon, Oxford, 2002