


Nächste Seite: Die Dichtematrix
Aufwärts: Spezifische Aspekte der Beschreibung
Vorherige Seite: Spezifische Aspekte der Beschreibung
Eine physikalische Observable 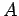 wird durch einem Hermitischen Operator
wird durch einem Hermitischen Operator 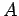 beschrieben:
beschrieben:
Die Zustände des Quantensystems kann man stets einem Hilbert-Vektoren
(Wellenfunktionen)
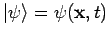 zuordnen.
zuordnen.
Reine Zustände (Anfangswertproblem):
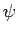 kann in eine orthonormale Basis der Eigensuständen entwickelt
werden:
kann in eine orthonormale Basis der Eigensuständen entwickelt
werden:
Matrizendarstellung eines Operators:
Die quantenmechanische Mittelwerte sind daher
Sei 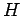 das Hamilton-Operator
das Hamilton-Operator
Dann
mit
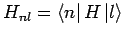 . Daher:
. Daher:
Man hat
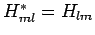 , da
, da 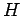 Hermitisch. Dann:
Hermitisch. Dann:
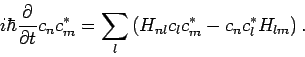 |
(23) |
Für einen beliebegen Operator 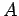 folgt dann
folgt dann
Alle Summationsindizes können umbennant werden, so dass folgt
(man kann auch sagen dass
![$\displaystyle i\hbar \frac{\partial }{\partial t}A=\left[H,A\right] _{-}$](img1140.png) ).
).
Prof. Igor Sokolov
2004-07-01
![]() wird durch einem Hermitischen Operator
wird durch einem Hermitischen Operator ![]() beschrieben:
beschrieben:
![]() kann in eine orthonormale Basis der Eigensuständen entwickelt
werden:
kann in eine orthonormale Basis der Eigensuständen entwickelt
werden:
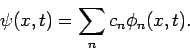
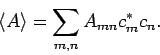
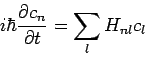
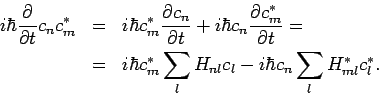
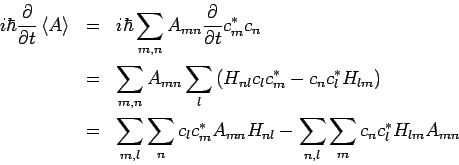
![\begin{eqnarray*}
i\hbar \frac{\partial }{\partial t}\left\langle A\right\rangle...
...t) \\
&\equiv &\left\langle \left[ H,A\right] _{-}\right\rangle
\end{eqnarray*}](img1139.png)
![$\displaystyle i\hbar \frac{\partial }{\partial t}A=\left[H,A\right] _{-}$](img1140.png) ).
).