


Nächste Seite: Analogien zur klassische Mechanik
Aufwärts: Spezifische Aspekte der Beschreibung
Vorherige Seite: Reine Zustände
Jetzt betrachten wir eine Gesamtheit von nichtwechselwirkenden Systemen
(Kopien), von gleicher Beschaffenheit, die sich unter gleichen
makroskopischen Bedingungen entwickeln: wir betrachten jetzt einen mikrokanonischen
Fall, in dem jedes System einem anderen mikroskopischen Anfangsbedingung
genügt. Für jede Kopie nimmt dann
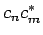 einen anderen Wert
an. Dann gilt
einen anderen Wert
an. Dann gilt
Die Matrix 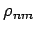 (entsprechenden Operator
(entsprechenden Operator 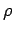 ) nennt man
Dichtematrix (statistische Operator). Die vorherige Gleichung kann man wie
folgt umschreiben:
) nennt man
Dichtematrix (statistische Operator). Die vorherige Gleichung kann man wie
folgt umschreiben:
Die Zeitentwichkung der Dichtematrix folgt aus Gl.(23): Mittelt man
die Gl über dem Ensemble, so erhält man
Diese Gleichung wird als quantenmechanische Analogie zur Liouville-Gleichung
angesehen. Statistischer Operator in Koordinatendarstellung:
Wenn die Dichtematrix nur die Fkt. der Energie ist, d.h.
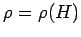 ,
dann ist
,
dann ist
![$\left[ H,\rho \right] =0$](img1149.png) und
und 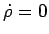 . Die Dichtematrix ist
diagonal in der Darstellung in der
. Die Dichtematrix ist
diagonal in der Darstellung in der 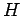 diagonal ist, so dass
diagonal ist, so dass
In diesem Fall kann 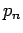 als Wahrscheinlichkeit angesehen werden, dass das
System sich in einem reinem Zustand
als Wahrscheinlichkeit angesehen werden, dass das
System sich in einem reinem Zustand 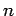 befindet, und
befindet, und
Eigenschaften der Dichtematrix:
 Hermitisch:
Hermitisch:
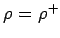 (klar aus der Definition)
(klar aus der Definition)

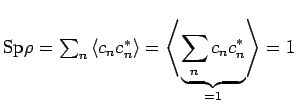 .
.
 Nicht-negativ definiert,
Nicht-negativ definiert,
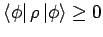 .
.
Unterabschnitte



Nächste Seite: Analogien zur klassische Mechanik
Aufwärts: Spezifische Aspekte der Beschreibung
Vorherige Seite: Reine Zustände
Prof. Igor Sokolov
2004-07-01
![]() einen anderen Wert
an. Dann gilt
einen anderen Wert
an. Dann gilt
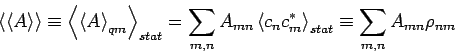
![\begin{eqnarray*}
i\hbar \frac{\partial }{\partial t}\rho _{nm} &=&i\hbar \frac{...
... _{lm}-\rho _{nl}H_{lm}\right) \equiv \left[
H,\rho \right] _{-}
\end{eqnarray*}](img1146.png)
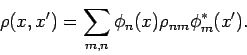
![]() ,
dann ist
,
dann ist
![]() und
und ![]() . Die Dichtematrix ist
diagonal in der Darstellung in der
. Die Dichtematrix ist
diagonal in der Darstellung in der ![]() diagonal ist, so dass
diagonal ist, so dass
![]() Hermitisch:
Hermitisch:
![]() (klar aus der Definition)
(klar aus der Definition)
![]()
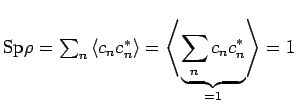 .
.
![]() Nicht-negativ definiert,
Nicht-negativ definiert,
![]() .
.