Denkbare Zustände: solche mit Energien zwischen ![]() und
und ![]() .
Zustände in der Energiedarstellung:
.
Zustände in der Energiedarstellung:
![]() :
:
![]() . Die Zustände bilden eine orthonormale Basis:
. Die Zustände bilden eine orthonormale Basis:
![]() ,
,
![]() . Im GG: Die Dichtematrix
. Im GG: Die Dichtematrix ![]() kommutiert mit dem
Hamilton-Operator
kommutiert mit dem
Hamilton-Operator ![]() ist diagonal in der Energiedarstellung:
ist diagonal in der Energiedarstellung:
![]() .
.
Postulat der gleichen a-priori Wahrscheinlichkeiten:
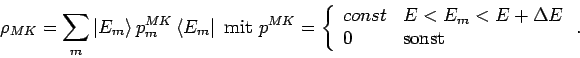
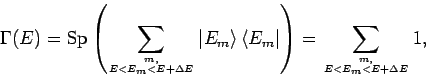
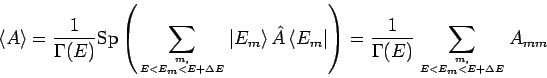
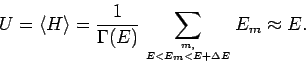
III Hauptsatz: Für ![]() ist
ist ![]() . Besitzt das System ein diskretes
Energiespektrum, so gibt es einen energetisch tiefsten Zustand
(Grundzustand). Für
. Besitzt das System ein diskretes
Energiespektrum, so gibt es einen energetisch tiefsten Zustand
(Grundzustand). Für
![]() wird dieser angenommen, so dass
wird dieser angenommen, so dass
![]() , mit
, mit ![]() - Entartungsgrad des Grundzustandes. Für
- Entartungsgrad des Grundzustandes. Für ![]() ist
ist ![]() (Nernst). Dieses Eigenschaft ist experimentell gut gestutzt.
Es wird daher angenommen, das wenn es eine Entartung gäbe (
(Nernst). Dieses Eigenschaft ist experimentell gut gestutzt.
Es wird daher angenommen, das wenn es eine Entartung gäbe (![]() )wird diese durch Phasenübergäge gebrochen.
)wird diese durch Phasenübergäge gebrochen.