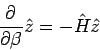Nächste Seite: Übergang zur klassischen Systeme.
Aufwärts: Dichtematrizen für die drei
Vorherige Seite: Mikrokanonische Gesamtheit: Isoliertes System.
Wir folgen hier dem Zugang der Kap.4.2. Andere Zugänge siehe Nolting,
Kap. 2.3.
Wir betrachten ein isoliertes System bestehend aus 2 Subsysteme in sehr
schwachen Kontakt: Das System 1, und das Wärmebad
(System 2). Die Schwache Wechselwirkung bedeutet, dass alle Zustände des
Systems nur sehr kleine Änderungen im Vergleich mit den Eigenzuständen des isolierten Systems erfahren.
Für das Gesamtsystem:
Alle Zustände des Gesamtsystems sind gleichwahrscheinlich. Für das
Gesamtsystem entspricht das Fixieren des Zustands 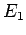 des kleineren Systems
des kleineren Systems
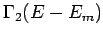 gleichwahrschenliche Möglichkeiten, so dass
gleichwahrschenliche Möglichkeiten, so dass
Da
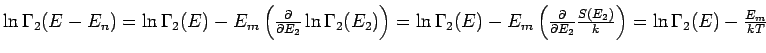 hat man
hat man
In Energiedarstellung hat man dann
I.A. hat man also
Normierung:
Der Nenner ist eigentlich die gleiche Zustandssumme, wie früher:
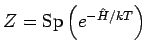 . Für die beliebige Observable
. Für die beliebige Observable 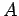
z.B.
(mit 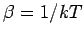 ). Die Freie Energie
). Die Freie Energie
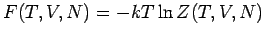 . Das
erlaubt die andere Schreibeweise der Dichtematrix:
. Das
erlaubt die andere Schreibeweise der Dichtematrix:
In der Koordinatendarstellung
so dass
Bemerkung: In einem Vielteilchensystem sind 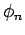 die Wellenfunktionen des ganzen Systems,
mit der entsprechenden Permutationseigenschaften (z.B. Bose oder Fermi).
die Wellenfunktionen des ganzen Systems,
mit der entsprechenden Permutationseigenschaften (z.B. Bose oder Fermi).
Die Bloch-Gleichung: Betrachten wir den Operator
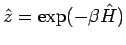 , genügt
, genügt
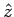 der folgenden Gleichung:
der folgenden Gleichung:
(die BLOCH-Gleichung) mit der Anfangsbedingung
(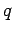 - Koordinaten, inklusive Spin,
- Koordinaten, inklusive Spin, 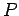 - Permutationsoperator).
- Permutationsoperator).
Unterabschnitte



Nächste Seite: Übergang zur klassischen Systeme.
Aufwärts: Dichtematrizen für die drei
Vorherige Seite: Mikrokanonische Gesamtheit: Isoliertes System.
Prof. Igor Sokolov
2004-07-01
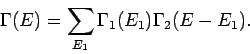
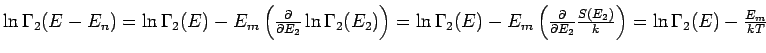 hat man
hat man
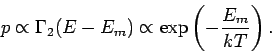
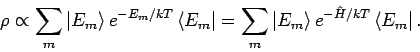
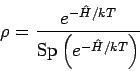
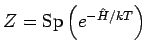 . Für die beliebige Observable
. Für die beliebige Observable 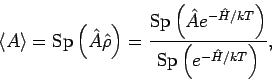
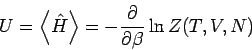
![\begin{displaymath}
\rho (x,x^{\prime })=\sum_{n}\phi _{n}^{*}(x^{\prime })\exp \left[ \beta
\left( F-\hat{H}\right) \right] \phi _{n}(x),
\end{displaymath}](img1244.png)
![]() , genügt
, genügt
![]() der folgenden Gleichung:
der folgenden Gleichung: