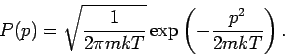Nächste Seite: Thermodynamische Störungstheorie
Aufwärts: Dichtematrizen für die drei
Vorherige Seite: Großkanonische Gesamtheit
Das Modell ist wichtig, da die Ansammlung harmonischer Oszillatoren ein
typisches Modell für viele Situationen ist (Moleküle, Einstein-Modell
eines Kristalls, u.s.w.). Wir betrachten den eindimensionalen Fall; die
Situation in höheren Dimensionen entspricht einem direkten Produkt
eindimensionale Dichtematrizen.
(Bemerkung: Parallel zu unserem Phononenbild, sind hier 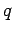 die
Normalkoordinaten, und
die
Normalkoordinaten, und 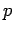 die entsprechende Impulse. Die Normalkoordinate
hat die Dimension
die entsprechende Impulse. Die Normalkoordinate
hat die Dimension
![$\left[ \mathrm{L}\cdot \mathrm{M}^{1/2}\right] $](img1296.png) .
Koordinate
.
Koordinate 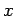 folgt als
folgt als 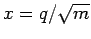 , wobei
, wobei 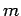 die Masse der Teilchen
ist).
die Masse der Teilchen
ist).
Die Energien der Zuständen sind
Bestimmen wir die Koordinaten-Dichtematrix des harmonischen Oszillators:
mit Normierungskonstante 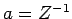 (die Wellenfunktionen in 1d sind
reell!), siehe Landau + Lifshitz, Band 5 §31.
(die Wellenfunktionen in 1d sind
reell!), siehe Landau + Lifshitz, Band 5 §31.
Wir berechnen die diagonalen und die nichtdiagonalen ''Elemente'' von 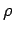 getrennt.
getrennt.
a) Diagonale: 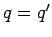 . Die Berechnung basiert auf einen Trick:
Berechnen wir zuerst
. Die Berechnung basiert auf einen Trick:
Berechnen wir zuerst
Da
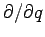 proportional zum Impulsoperator
proportional zum Impulsoperator
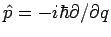 ist, und da der Impulsoperator für ein
harmonischen Oszillator die von 0 unterschiedlichen Matrizenelementen nur
zwischen die benachbarnten Zuständen besitzt, erhalten wir
ist, und da der Impulsoperator für ein
harmonischen Oszillator die von 0 unterschiedlichen Matrizenelementen nur
zwischen die benachbarnten Zuständen besitzt, erhalten wir
Da für ein harmonischen Oszillator gilt
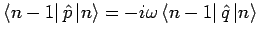 und
und
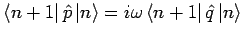 bekommen wir
bekommen wir
Unter der Benutzung der Tatsache, dass
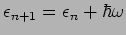 , dass
, dass
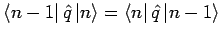 und dass
und dass
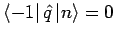 (die ''-1.'' Zustand
ist abwesend) erhalten wir
(die ''-1.'' Zustand
ist abwesend) erhalten wir
Auf analoge Weise findet man (unter Benutzung der rekurente Beziehungen
zwischen der Wellenfunktionen mit verschiedenen 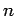 )
)
so dass
und deswegen
eine Gaussverteilung. Die Normierung
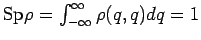 ergibt:
ergibt:
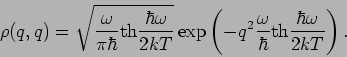 |
(24) |
b) Zur Berechnung der nichtdiagonale Elementen führen wir Koordinaten 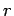 und
und 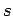 :
: 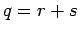 ,
,
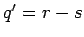 . Berechnen wir
. Berechnen wir
so dass
Auf analoge Weise findet man
so dass
und
Die Funktion 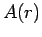 ist eigentlich schon bekannt, da für
ist eigentlich schon bekannt, da für 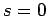 (am
''Diagonale'') ist
(am
''Diagonale'') ist
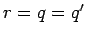 , so dass
, so dass 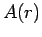 ist durch Gl.(24) mit
ist durch Gl.(24) mit 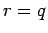 gegeben. Insgesamt erhält man
gegeben. Insgesamt erhält man
Bemerkung: Die diagonalen ''Elemente''
entsprechen der Wahrscheinlichkeitsdichte 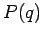 , einen Teilchen am Orte
, einen Teilchen am Orte 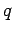 zu finden. Diese Wahrscheinlichkeit ist durch Gl.(24) gegeben, und
ist immer Gaußverteilt.
zu finden. Diese Wahrscheinlichkeit ist durch Gl.(24) gegeben, und
ist immer Gaußverteilt.
Für den Grenzfall
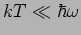 haben wir in ''richtige''
koordinate
haben wir in ''richtige''
koordinate 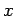
Das ist einfach die eintsprechende Quadrat der Wellenfunktion im
Grundzustand. Dagegen erhalten wir für
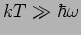
oder
(mit
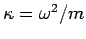 - die ''Federkonstante''), eine
Boltzmannverteilung.
In dem gleichen Limes verschwinden die nichtdiagonalenËlemente:
- die ''Federkonstante''), eine
Boltzmannverteilung.
In dem gleichen Limes verschwinden die nichtdiagonalenËlemente:
Da die Impulse und die Koordinaten des Harmonischen Oszillators symmetrisch
in den Hamilton-Operator eingehen (
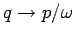 ), hat die
Dichtematrix im Impuls-Darstellung die gleiche Form. Im klassischen Fall
), hat die
Dichtematrix im Impuls-Darstellung die gleiche Form. Im klassischen Fall
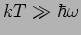 geht ihr Diagonalteil in die Maxwell-Verteilung über:
geht ihr Diagonalteil in die Maxwell-Verteilung über:



Nächste Seite: Thermodynamische Störungstheorie
Aufwärts: Dichtematrizen für die drei
Vorherige Seite: Großkanonische Gesamtheit
Prof. Igor Sokolov
2004-07-01
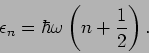
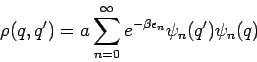
![]() getrennt.
getrennt.
![]() . Die Berechnung basiert auf einen Trick:
Berechnen wir zuerst
. Die Berechnung basiert auf einen Trick:
Berechnen wir zuerst
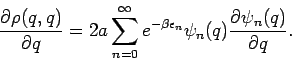
![\begin{displaymath}
\frac{\partial \psi _{n}(q)}{\partial q}=\frac{i}{\hbar }\le...
...\vert \hat{p}\left\vert n\right\rangle \psi _{n+1}(q)\right] .
\end{displaymath}](img1305.png)
![\begin{eqnarray*}
\frac{\partial \rho }{\partial q} &=&2a\sum_{n=0}^{\infty }e^{...
...t{q}\left\vert n\right\rangle \psi _{n+1}(q)\psi _{n}(q)\right]
\end{eqnarray*}](img1308.png)
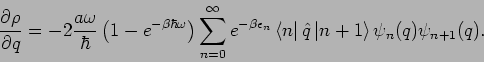
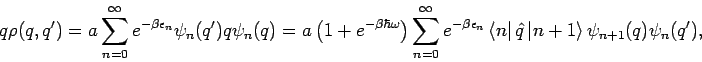
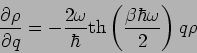
![\begin{displaymath}
\rho (q,q)=A\exp \left[ -q^{2}\frac{\omega }{\hbar }\mbox{th}\left( \frac{\beta
\hbar \omega }{2}\right) \right] ,
\end{displaymath}](img1315.png)
![]() und
und ![]() :
: ![]() ,
,
![]() . Berechnen wir
. Berechnen wir
![\begin{displaymath}
\frac{\partial \rho }{\partial s}=\frac{\partial \rho }{\par...
...{n}(q^{\prime })}{\partial q^{\prime }%
}\psi _{n}(q)\right] .
\end{displaymath}](img1320.png)
![\begin{displaymath}
\frac{\partial \rho }{\partial s}=-\frac{a\omega }{\hbar }\l...
...{n}(q^{\prime })-\psi _{n}(q)\psi _{n+1}(q^{\prime })\right] .
\end{displaymath}](img1321.png)
![\begin{displaymath}
s\rho (q,q^{\prime })=a\left( 1-e^{-\beta \hbar \omega }\rig...
..._{n}(q^{\prime })-\psi
_{n}(q)\psi _{n+1}(q^{\prime })\right]
\end{displaymath}](img1322.png)
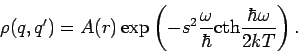
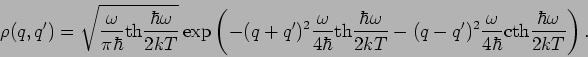
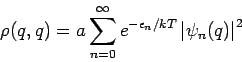
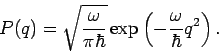
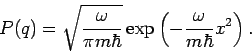
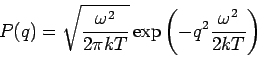
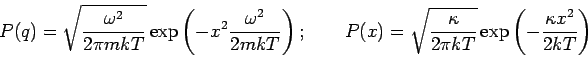
![]() ), hat die
Dichtematrix im Impuls-Darstellung die gleiche Form. Im klassischen Fall
), hat die
Dichtematrix im Impuls-Darstellung die gleiche Form. Im klassischen Fall
![]() geht ihr Diagonalteil in die Maxwell-Verteilung über:
geht ihr Diagonalteil in die Maxwell-Verteilung über: