Nächste Seite: Beispiel: Kanonische Dichtematrix für
Aufwärts: Dichtematrizen für die drei
Vorherige Seite: Übergang zur klassischen Systeme.
(Zustandsvariablen 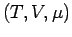 ). Das System
). Das System 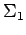 (das Hamilton-Operator
(das Hamilton-Operator 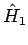 ) zusammen mit einem
viel größerem Bad (das Hamilton-Operator
) zusammen mit einem
viel größerem Bad (das Hamilton-Operator 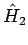 )
)
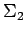 werden als Teile eines isolierten Systems
werden als Teile eines isolierten Systems 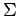 (das Hamilton-Operator
(das Hamilton-Operator 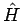 ) betrachtet.
Dabei wird angenommen das
) betrachtet.
Dabei wird angenommen das 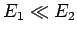 und
und 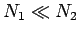 . Die Zuständen jedes Systems werden durch
Energien und Teilchenzahlen definiert:
. Die Zuständen jedes Systems werden durch
Energien und Teilchenzahlen definiert:
(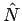 - ein Teilchenzahloperator), vorausgesetzt, dass die Teilchenzahl definiert ist, d.h.
- ein Teilchenzahloperator), vorausgesetzt, dass die Teilchenzahl definiert ist, d.h.
![$[\hat{H}_1,\hat{N}_1]_-=0$](img1278.png) .
Daher ist die Dichtematrix im Gleichgewicht
.
Daher ist die Dichtematrix im Gleichgewicht
(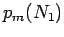 - Wahrscheinlichkeit des Zustands
- Wahrscheinlichkeit des Zustands 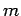 bei Teilchenzahl
bei Teilchenzahl 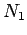 ).
Parallel zur klassischen Betrachtung: Die Gesamtzahl der Zustände
).
Parallel zur klassischen Betrachtung: Die Gesamtzahl der Zustände
Fixieren wir den Zustand von 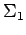 , so bleiben noch
, so bleiben noch
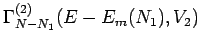 Möglichkeiten für die Auswahl des Zustandes von
Möglichkeiten für die Auswahl des Zustandes von 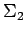 und damit von
und damit von 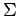 . Alle diese Zustände sind
a priori gleichwahrscheinlich. Parallel zur §... gilt
. Alle diese Zustände sind
a priori gleichwahrscheinlich. Parallel zur §... gilt
Es gilt:
Damit bleibt:
![$P_m(N_1) \propto \exp \left[ \displaystyle - \frac{1}{kT} \left( E_m(N_1) - \mu N_1 \right) \right]$](img1288.png) und
und
Die Normierung ergibt:
Der Nenner des Ausdrucks definiert die großkanonische Zustandssumme 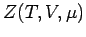 . In der
Energie-Teilchenzahl-Darstellung
. In der
Energie-Teilchenzahl-Darstellung
Gleich wie im klassischen Fall kann man auch schreiben
Hier ist 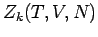 die kanonische Zustandssumme für das System mit
die kanonische Zustandssumme für das System mit 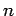 Teilchen, und
Teilchen, und
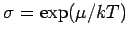 ist die Fugazität.
ist die Fugazität.



Nächste Seite: Beispiel: Kanonische Dichtematrix für
Aufwärts: Dichtematrizen für die drei
Vorherige Seite: Übergang zur klassischen Systeme.
Prof. Igor Sokolov
2004-07-01
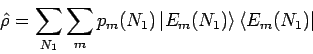
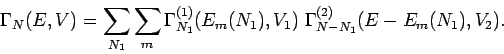
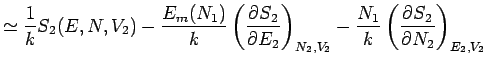
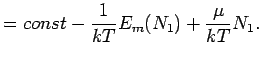
![$P_m(N_1) \propto \exp \left[ \displaystyle - \frac{1}{kT} \left( E_m(N_1) - \mu N_1 \right) \right]$](img1288.png) und
und
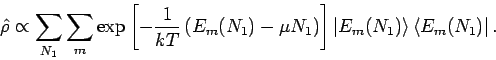
![\begin{displaymath}
\hat{\rho} = \frac{\exp \left[\displaystyle - \frac{1}{kT} \...
...- \frac{1}{kT} \left(\hat{H} - \mu \hat{N} \right) \right]} .
\end{displaymath}](img1290.png)
![\begin{displaymath}
Z(T,V,\mu)= \sum_{N=0}^\infty \sum_m \exp \left[ \displaystyle - \frac{1}{kT}
\left( E_m(N) - \mu N \right) \right]
\end{displaymath}](img1292.png)