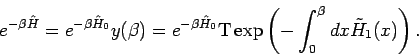Nächste Seite: Beispiel: Störungstheorie 2. Ordnung
Aufwärts: Thermodynamische Störungstheorie
Vorherige Seite: Thermodynamische Störungstheorie
Die Störungstheoretische Rechnungen sind ein wichtig Bestandteil der
Quantenmechanik, wobei die Eigenfunktionen/Werte eines Komplexen
Hamilton-Operators anhand der bekannten Näherungen aus der
entsprechenden Eigenschaften der bekannten, exakt lösbaren oder
einfacheren Modellen bestimmt werden können.
wobei 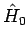 als ''freie'' Anteil ist, dessen Eigenwertproblem als gelöst anzusehen ist, und den Rest
als ''freie'' Anteil ist, dessen Eigenwertproblem als gelöst anzusehen ist, und den Rest 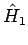 ist als Störung
anzusehen.
ist als Störung
anzusehen.
Ausgehend aus der Bloch-Gleichung betrachten wir einen noch nicht normierten
Operator
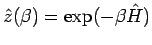 , so dass
, so dass
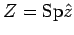 .
Dieser Operator gehorcht der DGl
.
Dieser Operator gehorcht der DGl
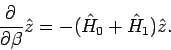 |
(25) |
Ansatz:
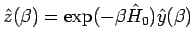 . Es gilt:
. Es gilt:
Vergleich mit Gl.(25) ergibt:
Daher
Das entspricht einer Art Wechselwirkungsdarstellung: für den Operator 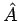
(vgl. mit Quantenmechanik
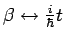 ):
):
Diese Gl. kann durch Iteration gelöst werden:
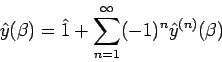 |
(26) |
mit
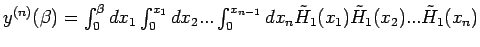 (mit
(mit
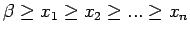 ). Eine kompakte Darstellung gelingt mit der Hilfe
des Ordnungsoperators
). Eine kompakte Darstellung gelingt mit der Hilfe
des Ordnungsoperators 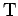 :
:
![$\hat{y}^{(n)}(\beta )=\frac{1}{n!}\int_{0}^{\beta }dx_{1}\int_{0}^{\beta
}dx_{2...
...left[ \tilde{H}_{1}(x_{1})\tilde{%
H}_{1}(x_{2})...\tilde{H}_{1}(x_{n})\right] $](img1361.png) . Eingesetzt in (26)
ergibt das
. Eingesetzt in (26)
ergibt das
(Für den Spezialfall, wenn 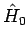 und
und 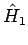 kommutieren,
bekommt man klarerweise
kommutieren,
bekommt man klarerweise
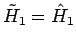 und
und
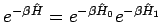 .)
.)



Nächste Seite: Beispiel: Störungstheorie 2. Ordnung
Aufwärts: Thermodynamische Störungstheorie
Vorherige Seite: Thermodynamische Störungstheorie
Prof. Igor Sokolov
2004-07-01
![]() , so dass
, so dass
![]() .
Dieser Operator gehorcht der DGl
.
Dieser Operator gehorcht der DGl
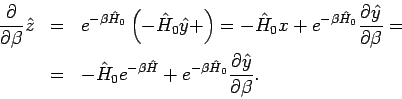
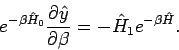
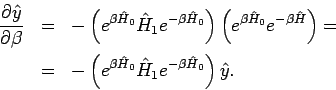
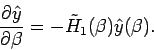
![\begin{displaymath}
\mathrm{T}\left[ A(x_{1})B(x_{2})\right] =\left\{
\begin{ar...
..._{2} \\
B(x_{2})A(x_{1}) & \mbox{sonnst}
\end{array}\right. :
\end{displaymath}](img1360.png)
![$\hat{y}^{(n)}(\beta )=\frac{1}{n!}\int_{0}^{\beta }dx_{1}\int_{0}^{\beta
}dx_{2...
...left[ \tilde{H}_{1}(x_{1})\tilde{%
H}_{1}(x_{2})...\tilde{H}_{1}(x_{n})\right] $](img1361.png) . Eingesetzt in (26)
ergibt das
. Eingesetzt in (26)
ergibt das