Nächste Seite: Über dieses Dokument ...
Aufwärts: Thermodynamische Störungstheorie
Vorherige Seite: Die thermodynamische Wechselwirkungsdarstellung
Die Lösung des ungestörten Problems:
Gesucht wird
Entwickeln wir
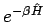 bis zur 2. Ordnung:
bis zur 2. Ordnung:
In thermodynamischer Wechselwirkungsdarstellung gilt i.A.:
Daher
Gleichermaßen gilt für die 2. Ordnung
Zur Ausrechnung von 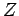 müssen die entsprechende Beiträge
aufsummiert werden. Dann verschwinden einige Glieder. Somit ist
müssen die entsprechende Beiträge
aufsummiert werden. Dann verschwinden einige Glieder. Somit ist
da dieser Ausdruck paarweise die Summanden mit entgegengesetzten Zeichen
enthält. Folglich gilt:
Dieses kann durch die Matrixelemente von 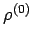 ausgedrückt werden:
ausgedrückt werden:

Die freie Energie
mit
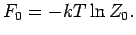 Bei der Berechnung von
Bei der Berechnung von 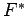 benutzen wir die
Tatsache, dass
benutzen wir die
Tatsache, dass
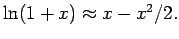 So ist
So ist
Das 1. und 4. Glied lässt sich durch den Mittelwert
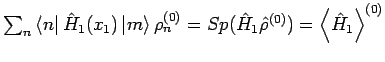 ausdrücken.
Das 2. und 3. Glied können zusammengefasst werden. Resultat:
ausdrücken.
Das 2. und 3. Glied können zusammengefasst werden. Resultat:
(Bemerkung: wir benutzen, dass
und (unter der Annahme des praktisch kontinuierlichen Spektrums) dass



Nächste Seite: Über dieses Dokument ...
Aufwärts: Thermodynamische Störungstheorie
Vorherige Seite: Die thermodynamische Wechselwirkungsdarstellung
Prof. Igor Sokolov
2004-07-01
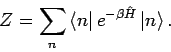
![\begin{eqnarray*}
Z &\approx &\sum_{n}e^{-\beta \epsilon _{n}}-\sum_{n}\left\lan...
..._{1})\tilde{H}_{1}(x_{2})\left\vert n\right\rangle -...\right] .
\end{eqnarray*}](img1368.png)
![\begin{displaymath}
\left\langle n\right\vert \int_{0}^{y}dx\tilde{H}_{1}(x)\lef...
..._{n}-\epsilon _{m})}-1\right] &
n\neq m
\end{array}\right. .
\end{displaymath}](img1370.png)
![\begin{eqnarray*}
&&\left\langle n\right\vert \int_{0}^{\beta }dx_{1}\int_{0}^{x...
...on _{n}-\epsilon _{m})}-1}{\epsilon
_{n}-\epsilon _{m}}\right] .
\end{eqnarray*}](img1371.png)
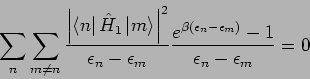
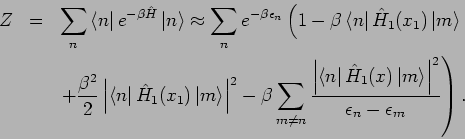
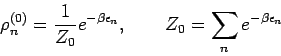
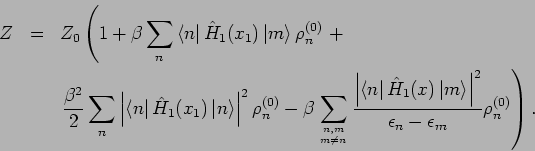
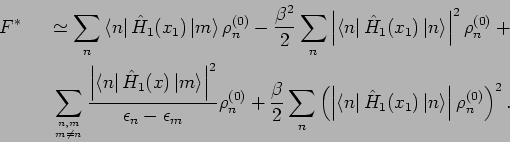
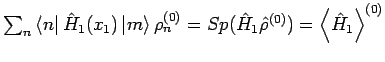 ausdrücken.
Das 2. und 3. Glied können zusammengefasst werden. Resultat:
ausdrücken.
Das 2. und 3. Glied können zusammengefasst werden. Resultat:
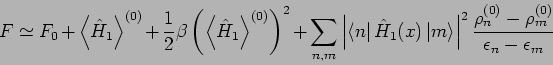
![\begin{displaymath}
\sum_{{n,m} \atop {m\neq n}} \frac{\left\vert \left\langle n...
...}-\epsilon _{m}}\left[ \rho _{n}^{(0)}-\rho _{m}^{(0)}\right]
\end{displaymath}](img1384.png)