Reflexion

Mit Hilfe der Fresnelschen Gleichungen ([Gerthsen et al., 86], [Hecht, 77]) lä\3t sich aus dem komplexen Brechungsindex eines Mediums die Reflektivität seiner Oberfläche unter verschiedenen Winkeln berechnen. Aufgrund der dielektrischen Eigenschaften des Mediums mu\3 dabei zwischen Strahlung unterschiedlicher Polarisationsrichtung unterschieden werden.

Entscheidend dabei ist, ob die Strahlung parallel zur Einfallsebene oder senkrecht zur Einfallsebene polarisiert ist. Die Einfallsebene wird dabei von zwei Vektoren in Richtung des einfallenden und des reflektierten Strahls aufgespannt (Abb. 2.14).

Für senkrechten Durchgang durch die Oberfläche () ergibt sich aus den Fresnel-Gleichungen für beliebige Polarisationsrichtungen das Verhältnis der reflektierten Strahlstärke zur einfallenden Strahlstärke :
 
Dies ist die bereits in Kapitel 2.4 eingeführte Reflektivität (2.27) der Oberfläche.

Für den Fall vereinfacht sich (2.71) zu
 
Das ist die klassische Beziehung für die Reflektivität in der Optik und gilt streng nur für ein transparentes Dielektrikum ().

Für die Wasseroberfläche liegt k bei Werten zwischen 0.001 und 0.6 für Wellenlängen zwischen 2m und 100m (siehe Abb. 2.16). Der Realteil des Brechungsindexes n nimmt dabei Werte zwischen 1.13 und 2.0 an. Für den empfindlichen Wellenlängenbereich der Radiance 1 Infrarotkamera ( = 3-5m) gilt n > 1.32 und k < 0.02. Damit gilt: . Die Wasseroberfläche verhält sich damit in guter Näherung wie ein transparentes Dielektrikum und Gleichung (2.72) gilt für Strahlung, die von der Kamera detektiert wird.

Unter dieser Bedingung ergibt sich die Winkelabhängigkeit der Reflektivität aus den klassischen Fresnel-Gleichungen [Gerthsen et al., 86]:
  
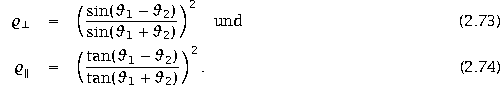
Dabei bezeichnen und die Reflektivität für Strahlung, die senkrecht, bzw. parallel zur Einfallsebene polarisiert ist. Die Winkel und ergeben sich nach dem Gesetz von Snellius (2.68) aus dem Realteil des Brechungsindexes n. Für sehr kleine Winkel (, ) ergeben beide Gleichungen (2.73) und (2.74) die Reflektivität für senkrechten Durchgang (2.72) als Grenzfall.

Für den speziellen Winkel ergibt sich für die parallele Polarisationsrichtung . Dies ist das bekannte Brewster'sche Gesetz und wird für diese Bedingung der Brewster-Winkel genannt. Damit wird Strahlung, die unter diesem Winkel auftrifft, keine Komponente mit dieser Polarisationsrichtung im reflektierten Anteil haben. Unpolarisierte Strahlung wird dabei polarisiert, wobei im reflektierten Anteil nur die Komponente mit senkrechter Polarisationsrichtung übrig bleibt.

Für unpolarisierte Strahlung definiert man die Reflektivität als arithmetisches Mittel der beiden Polarisationsrichtungen: