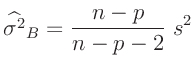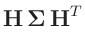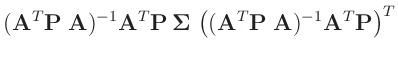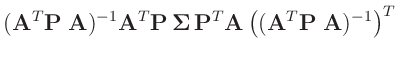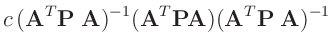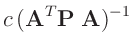- ... notwendig.1
- Zu den notwendigen Voraussetzungen für ein lineares Modell
gibt es unterschiedliche Auffassungen:
Martin (2012) Seite 145: Insbesondere ist die Annahme nicht
notwendig, dass die Fehler der Messwerte normalverteilt sind.
James (2006) Seite 186: Es werden keine Annahmen über die
Verteilung der Daten 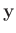 gemacht.
gemacht.
Nollau (1975) setzt schon bei der Herleitung des linearen
Modells für die
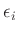 unabhängige normalverteilte
Zufallsgrößen voraus.
unabhängige normalverteilte
Zufallsgrößen voraus.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Erwartungswert2
- Im Unterschied zu Martin (2012)(Seite 145),
Fahrmeir (2009)(Seite 62) und Nollau (1975)(Seite
134) verwendet James (2006) in diesem Zusammenhang im Kapitel
8.4 (Seite 183ff) anstelle von
![$ \bm{\mathrm{E}}[y_i]$](img52.png) den
Ausdruck
den
Ausdruck
![$ \bm{\mathrm{E}}[y_i,\bm{\theta}]$](img53.png) .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Konstante3
- Bevington (2003) wählt im Kapitel 11 für die
Gewichte (Gleichung (11.2) Seite 194, Gleichung (11.32) Seite
203 sowie auf Seite 215) den Ausdruck:
Daraus folgt für die Konstante c:
Dies entspricht einer Normalisierung der Gewichtsfaktoren auf deren Mittelwert.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... damit:4
- Nach Fahrmeir (2009)( Seite 463 ) gilt für die
Linearkombination eines Zufallsvektors
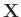 mit
einer geeignet dimensionierten Matrix
mit
einer geeignet dimensionierten Matrix 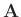 und einem geeignet
dimensionierten Vektor
und einem geeignet
dimensionierten Vektor 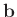 :
:
Damit ergibt sich mit
![$ \bm{\Sigma}=\bm{\mathrm{Cov}}[\bm{y}]$](img143.png) :
:
Mit
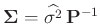 folgt daraus:
folgt daraus:
da die Matrizen 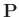 und
und
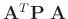 symmetrisch
sind.
symmetrisch
sind.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Maximum-Likelihood-Schätzung5
- Die Maximum-Likelihood-Schätzung
ist nicht erwartungstreu. Im allgemeinen wird sie deswegen durch die
Restringierte Maximum-Likelihood-Schätzung
ersetzt. (Fahrmeir (2009) Seite 94, Wakefield (2013)
Seite 44 ff.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Signifikanzniveau6
-
Im Praktikum wird meist mit
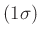 -Fehlerintervallen
gearbeitet. Das zugehörige Signifikanzniveau ist
-Fehlerintervallen
gearbeitet. Das zugehörige Signifikanzniveau ist 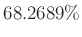 ,
woraus
,
woraus
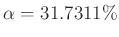 folgt.
folgt.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... t-Verteilung7
- Standard t-Verteilung
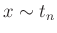 (z.B.Fahrmeir (2009) Seite 461)
(z.B.Fahrmeir (2009) Seite 461)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... bestimmt.8
- Zu bedingten Wahrscheinlichkeiten und zum Bayes-Theorem
siehe z.B. Koch (2000) (Kapitel 2) oder Wakefield (2013)
Kapitel 3
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... wird.9
- Die in den Gleichungen 10 und
11 genutzte, frei wählbare Konstante
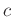 beeinflusst den Varianzfaktor
beeinflusst den Varianzfaktor 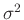 , der auch als Varianz
der Gewichtseinheit bezeichnet wird.
, der auch als Varianz
der Gewichtseinheit bezeichnet wird.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... umformen.10
-
Die Umformung erfolgt in mehreren Schritten. Dabei wird ausgenutzt,
dass die Gewichtsmatrix
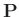 entsprechend ihrer Definition
symmetrisch ist. Daraus ergibt sich , dass auch die Matrix
entsprechend ihrer Definition
symmetrisch ist. Daraus ergibt sich , dass auch die Matrix
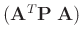 symmetrisch ist.
symmetrisch ist.
| entwickle: |
|
|
|
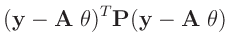 |
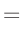 |
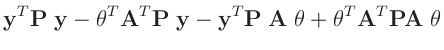 |
|
| alle Terme sind Skalare |
 |
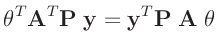 |
|
| |
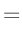 |
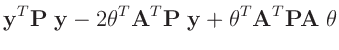 |
|
| mit: |
|
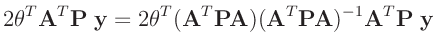 |
|
| und: |
|
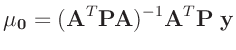 |
|
| |
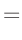 |
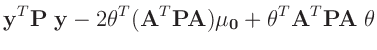 |
|
| setze: |
|
|
|
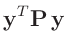 |
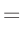 |
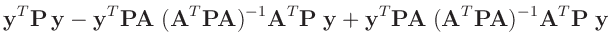 |
|
| |
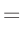 |
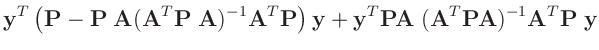 |
|
| aus |
|
|
|
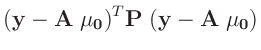 |
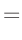 |
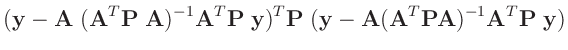 |
|
| |
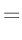 |
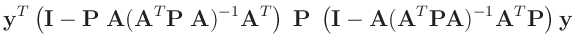 |
|
| |
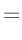 |
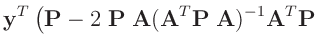 |
|
| |
|
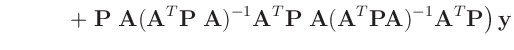 |
|
| |
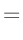 |
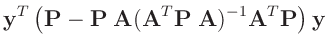 |
|
| und |
|
|
|
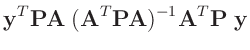 |
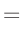 |
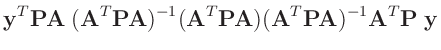 |
|
| |
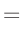 |
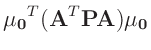 |
|
| folgt mit: |
|
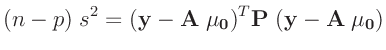 |
|
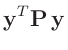 |
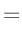 |
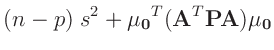 |
|
| damit ergibt sich: |
|
|
|
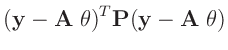 |
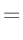 |
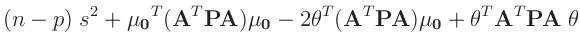 |
|
| |
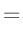 |
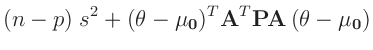 |
|
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Gammaverteilung11
-
Normal-inverse Gamma-Verteilung
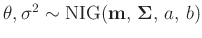
(z.B. Fahrmeir (2013) Seite 652):
Für die praktische Anwendung wird oftmals
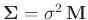 gesetzt und
gesetzt und
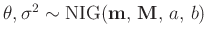 verwendet (z.B. Fahrmeir (2013) Seite 227).
verwendet (z.B. Fahrmeir (2013) Seite 227).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Gamma-Verteilung12
-
Inverse Gamma-Verteilung
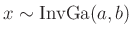
(z.B. Fahrmeir (2009) Seite 461):
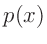 |
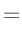 |
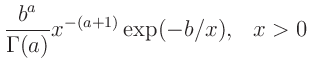 |
|
| mit: |
|
![$\displaystyle \bm{\mathrm{E}}[x] = \frac{b}{a-1}$](img289.png) |
|
| es gilt: |
 |
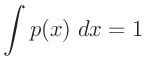 |
|
| daraus folgt: |
 |
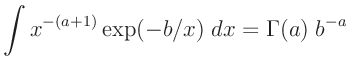 |
|
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
t-Verteilung13
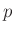 -dimensionale t-Verteilung
-dimensionale t-Verteilung
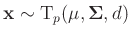
(z.B. Fahrmeir (2009) Seite 467)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Priori-Verteilungen14
- Zu der gleichen Verteilung
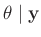 gelangt
Koch (2000)( Seite 111 ff) mit einer anderen
Priori-Verteilung. Er substituiert den Varianzfaktor
gelangt
Koch (2000)( Seite 111 ff) mit einer anderen
Priori-Verteilung. Er substituiert den Varianzfaktor 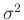 mit dem Gewichtsparameter
mit dem Gewichtsparameter
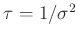 und benutzt die
Priori-Verteilungen
und benutzt die
Priori-Verteilungen
Daraus ergibt sich die Posteriori-Verteilung zu:
Der Exponent wird in der gleichen Weise umgeformt.
Damit lässt sich die Posteriori-Verteilung als Normal-Gammaverteilung
darstellen. Aus dieser folgt dann die mehrdimensionale t-Verteilung:
als Posteriori-Randverteilung für
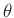 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...,15
- Fahrmeir (2013)(Seite 227ff.) verwendete als konjugierte
Priori-Verteilung eine Normal-inverse Gammaverteilung
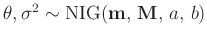 . Aus
dieser folgt als Posteriori-Verteilung wieder eine Normal-inverse
Gammaverteilung. Mit den von Fahrmeir (2013) auf Seite 231
angegebenen Werten
. Aus
dieser folgt als Posteriori-Verteilung wieder eine Normal-inverse
Gammaverteilung. Mit den von Fahrmeir (2013) auf Seite 231
angegebenen Werten
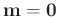 ,
,
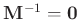 ,
, 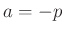 und
und
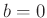 folgt als Priori-Verteilung:
folgt als Priori-Verteilung:
die nicht mit der von Fahrmeir (2013)(Gleichung. 4.16)
angestrebten, nichtinformativen Priori-Verteilung
übereinstimmt. Diese ist mit der Vorgabe 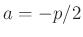 zu erreichen.
Daraus ergibt sich dann als Posteriori-Verteilung
zu erreichen.
Daraus ergibt sich dann als Posteriori-Verteilung
die sich durch die Normal-inverse Gammaverteilung
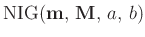 mit
mit
beschreiben lässt.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... werden16
- Wakefield (2013)(Seite 222) kommt auf eine inverse
Chi Quadrat Verteilung mit
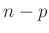 Freiheitsgraden
Freiheitsgraden
wobei zu beachten ist, dass Wakefield (2013) den
Parametervektor
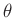 von
von
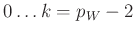 indiziert und
dort in
indiziert und
dort in 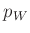 , der Anzahl der unbekannten Parameter,
, der Anzahl der unbekannten Parameter, 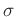 enthalten ist (Seite 209).
enthalten ist (Seite 209).
Der Erwartungswert der inversen Chi Quadrat Verteilung mit k
Freiheitsgraden ist gegeben durch
Daraus folgt:
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
abgeleitet17
- Bei der Herleitung wird ausgenutzt, dass die Matrizen
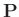 und
und
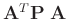 symmetrisch sind.
symmetrisch sind.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
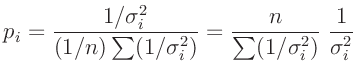
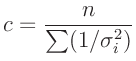
![$\displaystyle \bm{A}\,\bm{\mathrm{Cov}}[\bm{X}]\,\bm{A}^T$](img142.png)
![$\displaystyle \bm{\mathrm{Cov}}[\widehat{\bm{\theta}}]$](img144.png)
![$\displaystyle \bm{\mathrm{Cov}}[(\bm{A}^T\bm{P}\bm{A})^{-1}\,\bm{A}^T\bm{P}\,\bm{y}]$](img146.png)
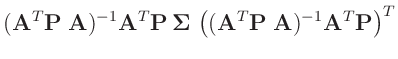
![$\displaystyle \bm{\mathrm{Cov}}[\widehat{\bm{\theta}}]$](img150.png)
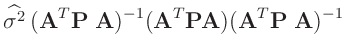
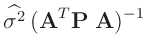
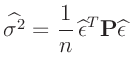
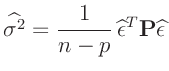
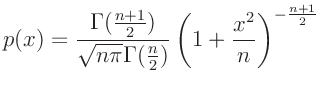
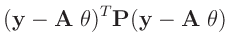
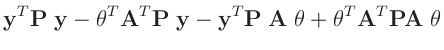
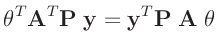
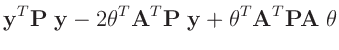
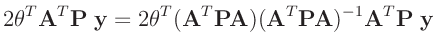
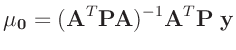
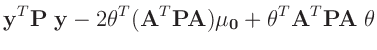
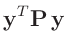
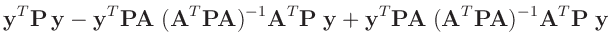
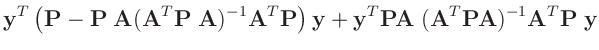
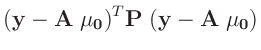
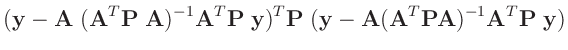
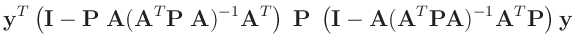
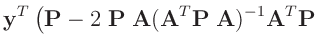
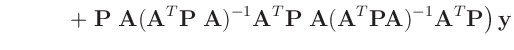
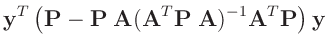
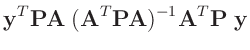
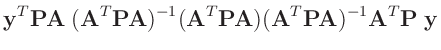
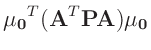
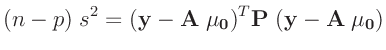
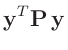
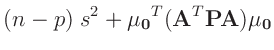
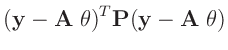
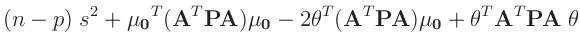
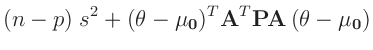
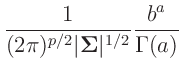
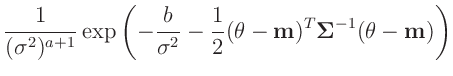
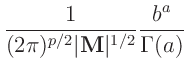
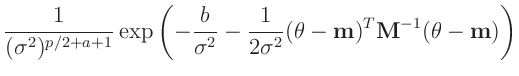
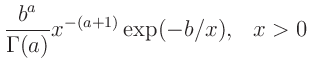
![$\displaystyle \bm{\mathrm{E}}[x] = \frac{b}{a-1}$](img289.png)
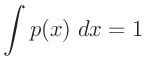
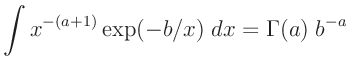
![$\displaystyle p(\bm{x}) =
\frac{\Gamma[(d+p)/2]}{\Gamma[d/2](d\;\pi)^{p/2}}\v...
...ac{(\bm{x}-\bm{\mu})^T\bm{\Sigma}^{-1}(\bm{x}-\bm{\mu})}{d}\right]^{-(d+p)/2}
$](img310.png)
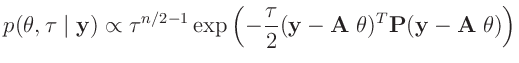
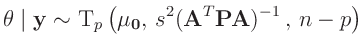
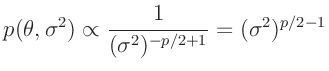
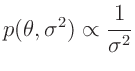
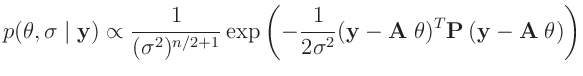
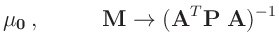
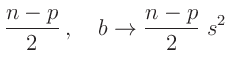
![$\displaystyle \bm{\mathrm{E}}[\chi^{-2}_k] =\frac{1}{k-2}
$](img388.png)