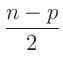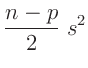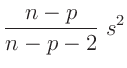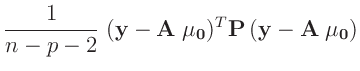Die Bayes Statistik verfolgt einen grundsätzlich anderen Ansatz als
die Klassische Statistik. Die Klassische Statistik versucht nur aus
den gegebenen Daten, den Messwerten, z.B. mit der Methode der
kleinsten Quadrate die wahrscheinlichsten Werte der unbekannten
Parameter zu schätzen, deren Erwartungswerte als fest angenommenen
werden. Demgegenüber geht die Bayes-Statistik davon aus, das auch die
Parameter selbst Zufallsgrößen sein können und bestimmt nicht nur die
Parameterwerte, für die die Datenwahrscheinlichkeit am größten ist,
sondern auch deren Wahrscheinlichkeitsverteilung, aus der sich die
Unsicherheit über den wahren Wert der Parameter ableiten lässt. Dazu
arbeitet die Bayes-Statistik mit bedingten Wahrscheinlichkeiten. Mit
Hilfe des Bayes-Theorem
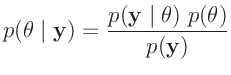 |
(16) |
wird die gesuchte bedingte Wahrscheinlichkeitsverteilung
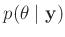 der Parameter, deren
Posteriori-Wahrscheinlichkeit bestimmt. 8Neben der Likelihood-Funktion
der Parameter, deren
Posteriori-Wahrscheinlichkeit bestimmt. 8Neben der Likelihood-Funktion
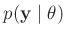 sind
Vorkenntnisse über die Wahrscheinlichkeitsverteilung der
unbekannten Parameter
sind
Vorkenntnisse über die Wahrscheinlichkeitsverteilung der
unbekannten Parameter
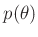 , über die sogenannte
Priori-Verteilung notwendig. Je nach Festlegung beinhaltet diese eine
mehr oder weniger große Subjektivität. Auch wenn die statistischen
Aussagen ausschließlich aus der Posteriori-Verteilung abgeleitet
werden, bleibt diese subjektive Komponente erhalten. Im Gegensatz dazu
arbeitet die klassische Statistik nur mit der Likelihood-Funktion.
Da der Ausdruck
, über die sogenannte
Priori-Verteilung notwendig. Je nach Festlegung beinhaltet diese eine
mehr oder weniger große Subjektivität. Auch wenn die statistischen
Aussagen ausschließlich aus der Posteriori-Verteilung abgeleitet
werden, bleibt diese subjektive Komponente erhalten. Im Gegensatz dazu
arbeitet die klassische Statistik nur mit der Likelihood-Funktion.
Da der Ausdruck
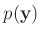 nur eine Normierungskonstanteist, reicht es aus, Gleichung 16 in der Form
nur eine Normierungskonstanteist, reicht es aus, Gleichung 16 in der Form
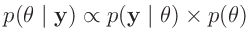 |
(17) |
zu verwenden.
In der Schreibweise der Bayes-Statistik lautet das allgemeine lineare Modell:
wobei im weiteren für die Verteilung der Messabweichungen eine mehrdimensionale
Normalverteilung vorausgesetzt wird.9Unter diesen Voraussetzungen ergibt sich die Likelihood-Funktion zu:
Da über die Parameter
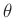 und
und 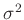 keine
Vorinformationen vorliegen, wird im weiteren von einem nichtinformativen
Priori-Verteilung ausgegangen. Für
keine
Vorinformationen vorliegen, wird im weiteren von einem nichtinformativen
Priori-Verteilung ausgegangen. Für 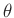 wird angenommen, das alle
möglichen Werte gleich wahrscheinlich sind.
wird angenommen, das alle
möglichen Werte gleich wahrscheinlich sind.
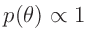 für
für
Da 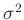 nur Werte im Intervall
nur Werte im Intervall
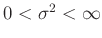 annehmen
kann, wird von einer Gleichverteilung für
annehmen
kann, wird von einer Gleichverteilung für
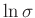 ausgegangen. Dies führt auf die nichtinformative Priori-Verteilung für
die Varianz:
ausgegangen. Dies führt auf die nichtinformative Priori-Verteilung für
die Varianz:
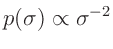 für
für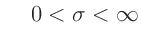
Somit ergibt sich für die Priori-Verteilung
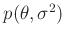 :
:
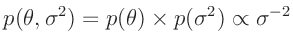 |
(19) |
Diese Verteilungsfunktion ist nicht normierbar und wird deswegen auch als
uneigentliche Priori-Verteilung bezeichnet. Da die verwendete
Likelihood-Funktion normierbar ist, folgt aus der Verknüpfung nach dem
Bayes-Theorem eine Posteriori-Verteilung, die normierbar ist.
Der Exponenten lässt sich geeignet umformen.10
Darin bedeuten
und
Damit ergibt sich eine Normal-inverse Gammaverteilung11
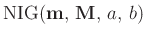 mit den Parametern
mit den Parametern
und der Dichte
![$\displaystyle p(\bm{\theta},\sigma\mid\bm{y}) \propto(\sigma^2)^{-(n+2)/2} \exp...
...eta}-\bm{\mu_0})^T\bm{A}^T\bm{P}\bm{A}\,(\bm{\theta}-\bm{\mu_0})\right]\right\}$](img281.png) |
(20) |
Um daraus die Verteilung
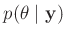 zu erhalten,
wird über
zu erhalten,
wird über 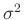 integriert.
integriert.
Der Integrand ist der Kern einer inversen Gamma-Verteilung12
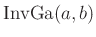 für
für 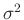 mit den Parametern
mit den Parametern
Aus dem Normierungsparameter der inversen Gamma-Verteilung folgt:
Dieser Ausdruck entspricht dem Kern einer 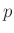 -dimensionalen
t-Verteilung13
-dimensionalen
t-Verteilung13
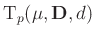 mit :
mit :
Für den Parametervektor
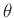 ergibt sich damit die
ergibt sich damit die 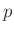 -dimensionalen t-Verteilung
-dimensionalen t-Verteilung
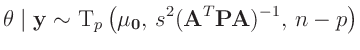 |
(21) |
als Posteriori-Randverteilung. Zu dem gleichen Ergebnis gelangt man auch mit anderen
nichtinformativen Priori-Verteilungen14,15. Aus dem Erwartungswert der mehrdimensionalen t-Verteilung
ergibt sich die Bayesschätzung
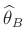 zu
zu
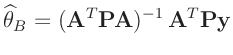 |
(22) |
Diese stimmt mit dem Ergebnis der Klassischen Statistik (12) überein.
Aus der Posteriori-Randverteilung (21) lässt sich der
Konfidenzbereich für jeden Teilvektor des Parametervektor
 und damit auch das Konfidenzintervall des einzelnen Parameters
und damit auch das Konfidenzintervall des einzelnen Parameters
 ableiten. Es ergibt sich dann eine eindimensionale
t-Verteilung mit
ableiten. Es ergibt sich dann eine eindimensionale
t-Verteilung mit 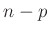 Freiheitsgraden, die sich mit der Substitution
Freiheitsgraden, die sich mit der Substitution
und dem entsprechenden Hauptdiagonalenelement der Dispersionsmatrix 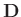
auf eine Standard t-Verteilung mit 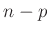 Freiheitsgraden zurückführen
lässt. Die sich daraus ergebenden Konfidenzintervalle
Freiheitsgraden zurückführen
lässt. Die sich daraus ergebenden Konfidenzintervalle
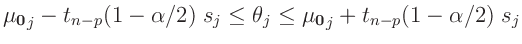 |
(23) |
stimmen mit denen der Klassischen Statistik (15) überein.
Aus der Posteriori-Verteilung (20) folgt als
Randverteilung für die Varianz 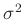 eine inverse
Gammaverteilung
eine inverse
Gammaverteilung
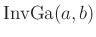 mit den Parametern
mit den Parametern
Aus dem Erwartungswert der inversen Gammaverteilung ergibt sich damit die
Bayesschätzung des Varianzfaktors
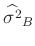 zu
zu
Das gleiche Ergebnis kann auch auf anderen Weise gefunden werden16. Die Bayesschätzung
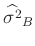 ist um den Faktor
ist um den Faktor
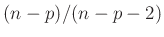 größer als die Schätzung
größer als die Schätzung
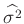 der
klassischen Statistik(13).
der
klassischen Statistik(13).
schaefer
2017-12-09
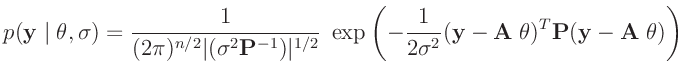
![]() und
und ![]() keine
Vorinformationen vorliegen, wird im weiteren von einem nichtinformativen
Priori-Verteilung ausgegangen. Für
keine
Vorinformationen vorliegen, wird im weiteren von einem nichtinformativen
Priori-Verteilung ausgegangen. Für ![]() wird angenommen, das alle
möglichen Werte gleich wahrscheinlich sind.
wird angenommen, das alle
möglichen Werte gleich wahrscheinlich sind.
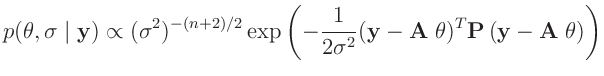
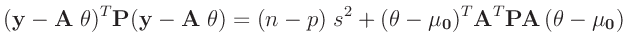
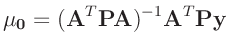
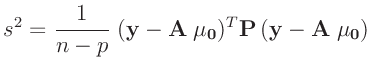
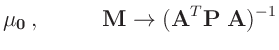
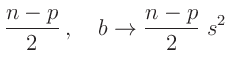
![$\displaystyle p(\bm{\theta}\mid\bm{y}) \propto \int (\sigma^2)^{-(n+2)/2} \exp ...
...0})^T\bm{A}^T\bm{P}\bm{A}\,(\bm{\theta}-\bm{\mu_0})\right] \right\} d\sigma^2
$](img284.png)
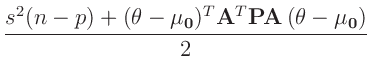
![$\displaystyle \Gamma(\frac{n}{2})\left[ \frac
{s^2(n-p)
+(\bm{\theta}-\bm{\mu_0})^T\bm{A}^T\bm{P}\bm{A}\,(\bm{\theta}-\bm{\mu_0})}{2}
\right]^{-\frac{n}{2}}$](img304.png)
![$\displaystyle \left[1 + \frac{(\bm{\theta}-\bm{\mu_0})^T\left(s^2(\bm{A}^T\bm{P}\bm{A})^{-1}\right)^{-1}(\bm{\theta}-\bm{\mu_0})}{n-p}\right]^{\frac{n-p+p}{2}}$](img306.png)
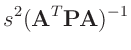
![]() und damit auch das Konfidenzintervall des einzelnen Parameters
und damit auch das Konfidenzintervall des einzelnen Parameters
![]() ableiten. Es ergibt sich dann eine eindimensionale
t-Verteilung mit
ableiten. Es ergibt sich dann eine eindimensionale
t-Verteilung mit ![]() Freiheitsgraden, die sich mit der Substitution
Freiheitsgraden, die sich mit der Substitution
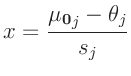
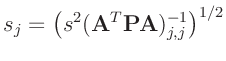
![]() eine inverse
Gammaverteilung
eine inverse
Gammaverteilung
![]() mit den Parametern
mit den Parametern