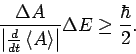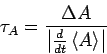Next: Wechselwirkungsbild.
Up: Heisenberg-Bild.
Previous: Evolution der Mittelwerte
Contents
Im Heisenberg-Bild ist die WF
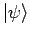 zeitunabhängig. Betrachten wir irgendeinen Operator
zeitunabhängig. Betrachten wir irgendeinen Operator  und führen wir die
Vektoren
und führen wir die
Vektoren
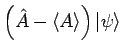 und
und
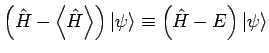 ein. Für diese zweie Vektoren wenden wir die
Schwarz-Ungleichung an (sieh Hausaufgabe ...). Man erhält
ein. Für diese zweie Vektoren wenden wir die
Schwarz-Ungleichung an (sieh Hausaufgabe ...). Man erhält
Da
![$\left[ \hat{A},\hat{H}\right] =i\hbar \frac{d}{dt}\left\langle
A\right\rangle $](img1829.png) , bekommen wir
, bekommen wir
oder
Der Wert
definirt die charakteristische Zeit der Evolution des Systems. Das ist die
Zeit während dessen sich der Mittelwert von 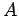 verschiebt um die
Verteilungsbreite (Varianz) von
verschiebt um die
Verteilungsbreite (Varianz) von 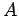 . Es gilt
. Es gilt
Nehmen wir jetzt das minimale 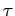 für alle mögliche Eigenschften
des Systems und assoziieren diese Zeit mit der charakteristischen
Evolutionszeit
für alle mögliche Eigenschften
des Systems und assoziieren diese Zeit mit der charakteristischen
Evolutionszeit 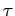 des Systems als solches. Für diese gilt auch
des Systems als solches. Für diese gilt auch
Wenn das System sich in einem stationären Zustand befindet, so ist für jedes 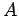
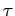 ist unendlich, und daher
ist unendlich, und daher 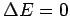 .
.
Prof. Igor Sokolov
2005-02-14
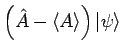 und
und
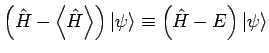 ein. Für diese zweie Vektoren wenden wir die
Schwarz-Ungleichung an (sieh Hausaufgabe ...). Man erhält
ein. Für diese zweie Vektoren wenden wir die
Schwarz-Ungleichung an (sieh Hausaufgabe ...). Man erhält
![]() zeitunabhängig. Betrachten wir irgendeinen Operator
zeitunabhängig. Betrachten wir irgendeinen Operator ![]() und führen wir die
Vektoren
und führen wir die
Vektoren
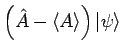 und
und
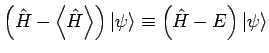 ein. Für diese zweie Vektoren wenden wir die
Schwarz-Ungleichung an (sieh Hausaufgabe ...). Man erhält
ein. Für diese zweie Vektoren wenden wir die
Schwarz-Ungleichung an (sieh Hausaufgabe ...). Man erhält
![$\left[ \hat{A},\hat{H}\right] =i\hbar \frac{d}{dt}\left\langle
A\right\rangle $](img1829.png) , bekommen wir
, bekommen wir