



Next: Bewegungsintegrale
Up: Unitäre Transformationen für die
Previous: Schrödinger-Bild.
Contents
In diesem Falle bleibt die Wellenfunktion zeitlich unverändert (d.h. sie
ist nur Anfangsbedingung),
Dann muss man gleichzeitig die Operatoren transformieren, anhand der allg.
Regel
damit alle Messbaren (Skalarprodukte, Matrizenelemente) unverändert bleiben.
Ist 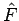 im Schrödinger-Bild zeitunabängig, so hängt
im Schrödinger-Bild zeitunabängig, so hängt
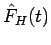 explizit von der Zeit ab;
explizit von der Zeit ab;
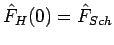 . Die
Änderung des Operators
. Die
Änderung des Operators 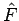 nach der endlichen Zeit
nach der endlichen Zeit 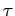 wird
durch die Formel
wird
durch die Formel
gegeben. Fangen wir bei 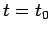 an. Wählen wir
an. Wählen wir 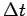 klein, so
gilt
klein, so
gilt
Nehmen wir
Daher bekommen wir
so dass
Wenn der Operator 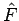 explizit von der Zeit abhängt, so gilt
explizit von der Zeit abhängt, so gilt
![\begin{displaymath}
\frac{d\hat{F}_{H}}{dt}=\frac{1}{i\hbar }\left[ \hat{F},\hat{H}\right] +%
\frac{\partial \hat{F}}{\partial t}.
\end{displaymath}](img1803.png) |
(47) |
Subsections
Prof. Igor Sokolov
2005-02-14
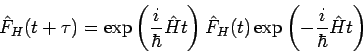
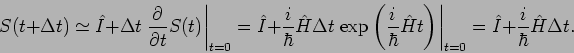
![\begin{displaymath}
\frac{d\hat{F}_{H}}{dt}=\frac{i}{\hbar }\left[ \hat{H},\hat{F}\right] =\frac{%
1}{i\hbar }\left[ \hat{F},\hat{H}\right] .
\end{displaymath}](img1802.png)