



Next: Etwas andere Schreibeweise
Up: Nichtentartetes Spektrum
Previous: Nichtentartetes Spektrum
Contents
Der direkte Weg hier ist die Zustände in der Energiedarstellung des
ungestörten Systems zu beschreiben:
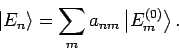 |
(50) |
Betrachten wir die Gleichung
und setzen wir die Entwicklung, Gl.(50), ein:
Da
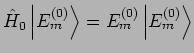 bekommen wir
bekommen wir
Um das entsprechende Gleichungssystem explizit zu bekommen bilden wir ein
Skalarprodukt mit
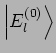 :
:
oder
Das ergibt ein Gleichungssystem für die Entwicklungskoeffizienten:
wobei
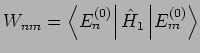 die Matrizenelementen der Störung sind.
die Matrizenelementen der Störung sind.
Die Entwicklung, Gl.(49) entspricht dann
(mit
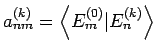 ).
Setzen wir das in unser Gleichungssystem ein, so erhalten wir für
).
Setzen wir das in unser Gleichungssystem ein, so erhalten wir für 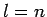
Der Vergleich der Glieder mit gleichen Potenzen von 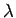 ergibt:
ergibt:
Da
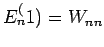 , bekommen wir aus der 2. Gleichung
, bekommen wir aus der 2. Gleichung
die Werte von 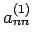 bleiben unbestimmt.
Betrachten wir nun
bleiben unbestimmt.
Betrachten wir nun 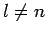 so erhalten wir
so erhalten wir
Aus 1. Gleichung des 2. System bekommen wir in der 1. Näherung
so dass die Wellenfunktion in der 1. Näherung ist
Wir setzen voraus, das die Wellenfunktionen in jeder Näherung
normiert werden müssen. Der Wert 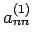 ist dann aus der
Normierungsbedingung zu finden:
ist dann aus der
Normierungsbedingung zu finden:
Daher gilt
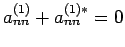 :
: 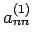 ist rein
imaginär. Da die Wellenfunktion nur bis zu einem Phasenfaktor bestimmt
wird, können wir
ist rein
imaginär. Da die Wellenfunktion nur bis zu einem Phasenfaktor bestimmt
wird, können wir 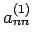 als reell voraussetzen und gleich 0
annehmen. Daher
als reell voraussetzen und gleich 0
annehmen. Daher
Bemerkung 1: Daraus folgt, dass in der 1. Ordnung für die WF
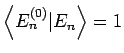 , d.h.
, d.h. 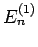 ist
orthogonal zu
ist
orthogonal zu 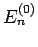 .
.
Unter Benutzung der Werte von 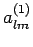 erhalten wir aus dem 1.
Gleichungssystem
erhalten wir aus dem 1.
Gleichungssystem
Wichtig: Die Korrektur 2. Ordnung zur Energie des Grundzustandes
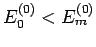
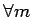 ist stets negativ.
ist stets negativ.
Insgesamt lautet die Energie in der 2. Ordnung der Störungstheorie
(jetzt in jeder beliebigen Darstellung, da die Matrizenelementen
darstellungsunabhängig sind) unter Voraussetzung 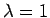
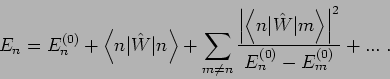 |
(51) |
Gleichermassen bekommt man auch die höheren Näherungen. Wir werden
später ein ''automatisiertes'' Schema dafür entwickeln. Damit die
Resultate der Störungstheorie möglichst gut sind, soll die
Störung 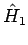 möglichst ''klein'' sein (im Sinne seiner
Matrizenelementen). Es ist sehr vorteilhaft, wenn die Energieabstände im
ungestörten System möglicht groß sind. Am besten soll
möglichst ''klein'' sein (im Sinne seiner
Matrizenelementen). Es ist sehr vorteilhaft, wenn die Energieabstände im
ungestörten System möglicht groß sind. Am besten soll
gelten.
Bemerkung 2: Da
gilt
Aus der Normierung (Bemerkung 1) folgt dass in der 2. Ordnung in Energie (1.
Ordnung in WF)
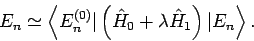 |
(52) |




Next: Etwas andere Schreibeweise
Up: Nichtentartetes Spektrum
Previous: Nichtentartetes Spektrum
Contents
Prof. Igor Sokolov
2005-02-14
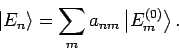
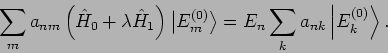
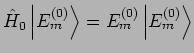 bekommen wir
bekommen wir
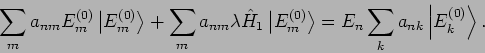
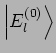 :
:
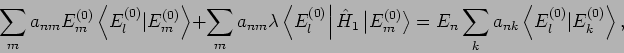
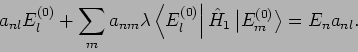
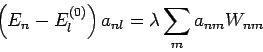
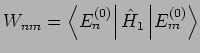 die Matrizenelementen der Störung sind.
die Matrizenelementen der Störung sind.
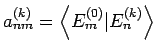 ).
Setzen wir das in unser Gleichungssystem ein, so erhalten wir für
).
Setzen wir das in unser Gleichungssystem ein, so erhalten wir für 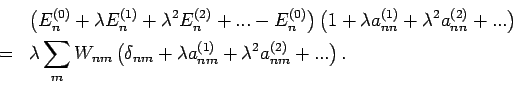
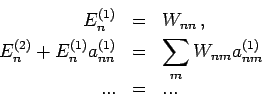
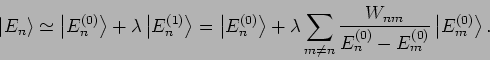
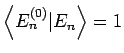 , d.h.
, d.h. ![]() erhalten wir aus dem 1.
Gleichungssystem
erhalten wir aus dem 1.
Gleichungssystem
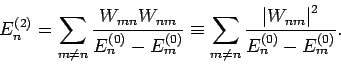
![]()