Für die Berechnung der Korrektur zur Energie des ![]() -ten stationären
Zuständes muß man die Energieniveaus
-ten stationären
Zuständes muß man die Energieniveaus ![]() und die
Wellenfunktionen
und die
Wellenfunktionen ![]() des ungestörten Systems (für die
Matrizenelementen) möglichst genau kennen. Es ist aber oft so, dass nur
die ersten angeregten Zustände eines ungestörten System hinreichend
gut bekannt sind (durch numerische Rechnung der Schrödingergl. oder durch
Variationsverfahren). Man kann die Formel der Störungstheorie so
umformen, das bei den Berechnungen für die niedrigen Niveaus die Rolle
der höher liegenden Niveaus vermindert wird. Führen wir die
identische Umformung
des ungestörten Systems (für die
Matrizenelementen) möglichst genau kennen. Es ist aber oft so, dass nur
die ersten angeregten Zustände eines ungestörten System hinreichend
gut bekannt sind (durch numerische Rechnung der Schrödingergl. oder durch
Variationsverfahren). Man kann die Formel der Störungstheorie so
umformen, das bei den Berechnungen für die niedrigen Niveaus die Rolle
der höher liegenden Niveaus vermindert wird. Führen wir die
identische Umformung
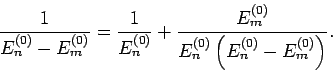
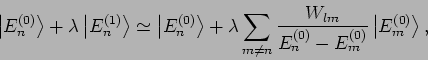
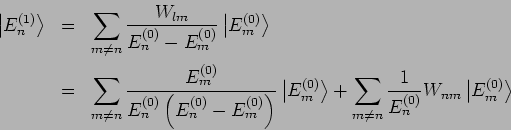
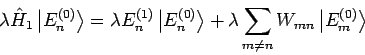
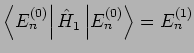 ). Daher
). Daher
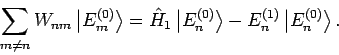
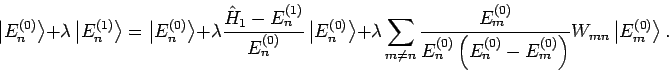
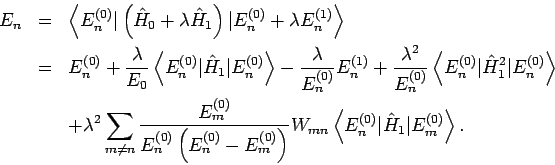
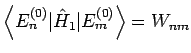 und
und
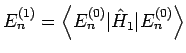 bekommen wir (
bekommen wir (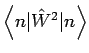 können
wir auch als eine Summe ausschreiben:
können
wir auch als eine Summe ausschreiben: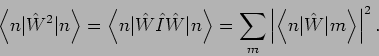
Es sind auch viele andere Umformungen möglich, die möglicherweise die Konvergenz der Reihen beschleunigen. Die folgen aus einer allgemeinen Grundformel für die Störungstheorie (später).