Einführende Bemerkungen

Seriös genommen, sind die meisten Quantensysteme Vielteilchensysteme; sogar das Wasserstoffatom besteht aus einem Elektron und einem Kern (Proton), dass wir in unseren früheren Ausführungen als unbewegliches Zentrum angenommen haben. Solche Sysrteme sind durch die Wellenfunktionen beschrieben, die von den Koordinaten aller Teilchen abhängig sind:

$$\Psi (\mathbf{r}_{1},\mathbf{r}_{2},\mathbf{r}_{3},...,t).$$

Das Betragsquadrat der Wellenfunktion

$$\left\vert \Psi (\mathbf{r}_{1},\mathbf{r}_{2},\mathbf{r}_{3... ...ert ^{2}=P(\mathbf{r}_{1},\mathbf{r}_{2},\mathbf{r}_{3},...,t)$$

gibt uns die Wahrscheinlichkeitsdichte, das Teilchen 1 im Volumenelement um $% \mathbf{r}_{1}$, das Teilchen 2 im Volumenelement um $\mathbf{r}_{2}$ u.s.w. zu finden. Der 3N-dimensionale Raum der Koordinaten aller Teilchen ist der Konfigurationsraum des Systems. Im Weiteren betrachten wir als Beispiel die Zweiteilchensysteme. Die Normierung der WF erfolgt durch

$$\int \left\vert \Psi (\mathbf{r}_{1},\mathbf{r}_{2},\mathbf{... ...t\vert ^{2}d\mathbf{r}_{1}d\mathbf{r}_{2}d\mathbf{r}_{3}...=1.$$

Die Normierung der WF bleibt in der Zeit erhalten (falls der Hamiltonian Hermite'sch ist). Die Wahrscheinlichkeitsdichte der Position von Teilchen 1, wenn die Position von Teilchen 2 nicht fixiert ist, ist

$$P(\mathbf{r}_{1})=\int P(\mathbf{r}_{1},\mathbf{r}_{2})d\mathbf{r}_{2}$$

das gibt uns die Verteilung der Messresultaten bei der Messung der Position von Teilchen 1, wenn keine Messung am Teilchen 2 vorgenommen wird.

Das gleiche gilt für die WF in der Impulsdarstellung:

$$\Psi(\mathbf{p}_1,\mathbf{p}_2, \mathbf{p}_3,...,t) = (2\pi ... ...N \mathbf{r}_j \mathbf{p}_j \right) \prod_i d \mathbf{r}% _i.$$

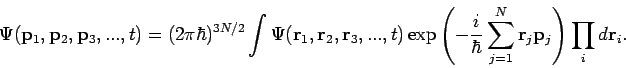
In einigen Situationen kann die Wellenfunktion als Produkt $\Psi (\mathbf{r}% _{1},\mathbf{r}_{2})=\Psi (\mathbf{r}_{1})\Psi (\mathbf{r}_{2})$ dargestellt werden (die ist faktorisiert). Die WF in Impulsdarstellung ist in diesem Fall ebenso faktorisiert. Für eine faktorisierte WF, wenn man sich für die Einteilchenmittelwerte ( $\left\langle \mathbf{r}% _{1}\right\rangle$, $\left\langle \mathbf{r}_{1}^{2}\right\rangle$, $% \left\langle \mathbf{p}_{1}\right\rangle$ u.s.w.) interessiert, kann man die über die Einteilchenwellenfunktion $\Psi (\mathbf{r}_{1})$ ausrechnen, und die Existenz von Teilchen 2 einfach ingnorieren.

Wenn die Teilchen nicht wechselwirken, d.h. wenn der Hamiltonian des Systems als Summe $\hat{H}=\hat{H}_{1}+\hat{H}_{2}$ geschrieben werden kann, wobei $\hat{H}_{1}$ nur auf die Funktionen von $\mathbf{r}_{1}$ und $\hat{H}_{2}$ nur auf die Funktionen von $\mathbf{r}_{2}$ einwirkt, und wenn zur Zeit $t=0$ die WF des System faktorisiert war $\Psi (\mathbf{r}_{1},\mathbf{r}_{2},0)=\Psi (\mathbf{r}% _{1},0)\Psi (\mathbf{r}_{2},0)$, so bleibt sie immer faktorisiert. Betrachten wir die Ls'gen

$$i\hbar \frac{\partial }{\partial t}\Psi (\mathbf{r}_{1},t)=\hat{H}_{1}\Psi (% \mathbf{r}_{1},t)$$

und

$$i\hbar \frac{\partial }{\partial t}\Psi (\mathbf{r}_{2},t)=\hat{H}_{2}\Psi (% \mathbf{r}_{2},t)$$

mit der entsprechenden Anfangsbedingungen. Es gilt:

$$\begin{eqnarray*} i\hbar \frac{\partial }{\partial t}\Psi (\mathbf{r}_{1},\mathb... ...\mathbf{r}_{2},t)=\hat{H}\Psi (\mathbf{r}_{1},\mathbf{r}_{2},0). \end{eqnarray*}$$

Die Wechselwirkung zwischen den Teilchen stört die Faktorisierung im Laufe der Zeit.

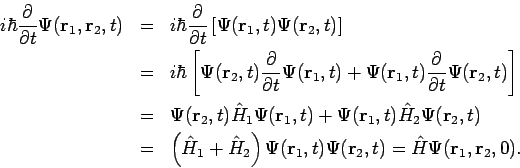
Solche Zusammenhänge kann man auch in anderen Darstellungen feststellen.