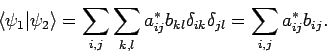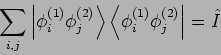Hier erläutern wir eine oft benutzte Operation der Erzeugung der Hilberträume der Zuständen der Systeme mehrere Teilchen.
Betrachten wir als Beispiel zunächst ein System aus 2 Teilchen. Ein
Produkt der WF zweier Teilchen
![]() stellt einen speziellen Zustand dieses Systems dar. I.A. faktorisieren nicht
die Wellenfunktionen, die faktorisierte WF'nen bilden aber eine VONS der
Funktionen in einem Hilbertraum alle Zuständen: Die allgemeine WF
stellt einen speziellen Zustand dieses Systems dar. I.A. faktorisieren nicht
die Wellenfunktionen, die faktorisierte WF'nen bilden aber eine VONS der
Funktionen in einem Hilbertraum alle Zuständen: Die allgemeine WF
![]() kann als lineare Kombination solcher
Produkte dargestellt werden: Die WF kann (als Fkt. von
kann als lineare Kombination solcher
Produkte dargestellt werden: Die WF kann (als Fkt. von
![]() , bei
festgehaltenen
, bei
festgehaltenen
![]() ) über VONS der Funktionen von
) über VONS der Funktionen von
![]() entwickelt werden:
entwickelt werden:
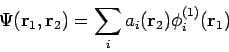
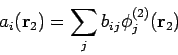
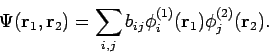
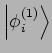 ) und
) und
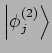 ).
).
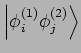 sind
die Elemente weder von
sind
die Elemente weder von 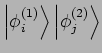 und aus allen möglichen ihrer
Linearkombiantionen, d.h. aus der Funktionen
und aus allen möglichen ihrer
Linearkombiantionen, d.h. aus der Funktionen
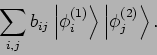
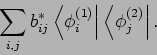
Das Skalarprodukt der reinen Produktzustände
![]() und
und
![]() (
(
![]() ,
,
![]() ) ist
folgendermassen definiert:
) ist
folgendermassen definiert:
Das Skalarprodukt der allgemeinen Zustände
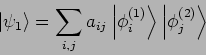
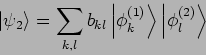
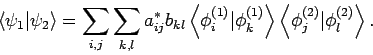
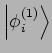 und
und
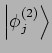 die VONS den Funktionen in
die VONS den Funktionen in 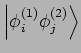 ein VONS in
ein VONS in
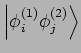 gilt:
gilt: