



Next: About this document ...
Up: Symmetrische und antisymmetrische Wellenfunktionen
Previous: Symmetrische und antisymmetrische Wellenfunktionen
Contents
Betrachten wir z.B. einen Zustand eines 2-Elektronensystems, das in einem
Singulettzustand präpariert ist.
Konzentrieren wir uns auf den Spinanteil so ist der Hilbertraum das Tensorprodukt
zweier zweidimensionalen Hilberträumen für die entsprechende Spins:
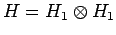 (
(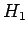 -Hilbertraum der Einteilchenzustände). Als
Basis in
-Hilbertraum der Einteilchenzustände). Als
Basis in 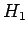 können wir die Eigenfunktionen von
können wir die Eigenfunktionen von
benutzen: Die Basisvektoren sind
Jeden Vektor in dem Hilbertraum kann man als lineare Kombination der
Basisvektoren darstellen. So z.B. die Eigenvektoren von
sind
und
Der Spinanteil an der Gesamtwellenfunktion in einem Singulett ist
Diese Funktion lässt sich gleichfalls auch als
schreiben.
Die Spinzustände der Elektronen im Singulett sind verschränkt
(entangled): Die Messung von 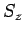 am Elektron 1 (einem am Orte
am Elektron 1 (einem am Orte 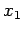 ,
das dem Beobachter A, Alice zu Verfügung steht; i.A. numerieren
die Indizes nicht die Elektronen, sondern die Beobachtungsorte!) ergibt mit
der gleichen Wahrscheinlichkeit die Werte
,
das dem Beobachter A, Alice zu Verfügung steht; i.A. numerieren
die Indizes nicht die Elektronen, sondern die Beobachtungsorte!) ergibt mit
der gleichen Wahrscheinlichkeit die Werte 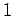 und
und 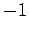 . Das Zustand nach dem
Messung kann dann so definiert werden: Ergibt die Messung 1, was mit der
Wahrscheinlichkeit
. Das Zustand nach dem
Messung kann dann so definiert werden: Ergibt die Messung 1, was mit der
Wahrscheinlichkeit 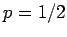 da
da
ist das Zustand von Teilchen 2 (von Beobachter B, Bob) ist auch
fixiert, und der ist
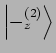 . Ergibt die Messung
. Ergibt die Messung 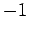 , so wird das Zustand der Teilchen 2
, so wird das Zustand der Teilchen 2
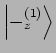 .
.
Nehmen wir an, dass Alice nicht 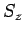 sondern
sondern 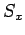 misst. In diesem
Fall, wenn sie 1 bekommt, so ist der Zustand von Teilchen 2
misst. In diesem
Fall, wenn sie 1 bekommt, so ist der Zustand von Teilchen 2
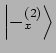 sonst ist es
sonst ist es
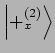 .
Da das Elektron 2 nicht gleichzeitig einen scharfen Wert von
.
Da das Elektron 2 nicht gleichzeitig einen scharfen Wert von 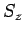 und
und 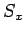 haben kann (Vertauschungsbedingung
haben kann (Vertauschungsbedingung  Unschärferelation) muss man annehmen, das sein Spinzustand vor der Messung
nicht definiert ist:
Unschärferelation) muss man annehmen, das sein Spinzustand vor der Messung
nicht definiert ist:
Ein Paar  zwei Stück.
zwei Stück.
Experimentell wird dieses Verhalten für ein anderes System nachgewiesen:
für einen Biphoton (zwei Photonen in einem Singulettztstand, mit
entsprechendem antisymmetrisiertem räumlichen Anteil der Wellenfunktion die
2 in entgegengesetzten Richtungen laufenden Wellen entspricht).




Next: About this document ...
Up: Symmetrische und antisymmetrische Wellenfunktionen
Previous: Symmetrische und antisymmetrische Wellenfunktionen
Contents
Prof. Igor Sokolov
2005-02-14
![]() (
(![]() -Hilbertraum der Einteilchenzustände). Als
Basis in
-Hilbertraum der Einteilchenzustände). Als
Basis in ![]() können wir die Eigenfunktionen von
können wir die Eigenfunktionen von
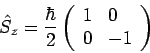
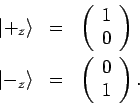
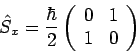
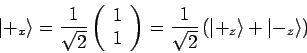
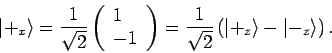
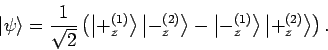
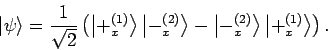
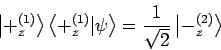
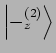 . Ergibt die Messung
. Ergibt die Messung 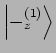 .
.
![]() sondern
sondern ![]() misst. In diesem
Fall, wenn sie 1 bekommt, so ist der Zustand von Teilchen 2
misst. In diesem
Fall, wenn sie 1 bekommt, so ist der Zustand von Teilchen 2
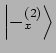 sonst ist es
sonst ist es
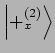 .
Da das Elektron 2 nicht gleichzeitig einen scharfen Wert von
.
Da das Elektron 2 nicht gleichzeitig einen scharfen Wert von ![]() und
und ![]() haben kann (Vertauschungsbedingung
haben kann (Vertauschungsbedingung ![]() Unschärferelation) muss man annehmen, das sein Spinzustand vor der Messung
nicht definiert ist:
Unschärferelation) muss man annehmen, das sein Spinzustand vor der Messung
nicht definiert ist: