Symmetrische und antisymmetrische Wellenfunktionen

Die allg. Ls'gen der Schrödinger-Gl. können bestimmte Symmetrie haben, oder auch nicht. Von allen Ls'gen darf man für die Bosonensysteme nur die Lösungen verwenden, die zu symmetrischen Funktionen (über alle Variablen, inklusive Spin) gehören, für die Fermionensysteme nur den antisymmetrische Funktionen angehören. Bis zu einem Normierungsfaktor ist die symmetrische Funktion für 2 Teilchen

$$\psi _{s}=A\left[ \psi (1,2)+\psi (2,1)\right]$$

und die antisymmetrische Funktion

$$\psi _{a}=B\left[ \psi (1,2)-\psi (2,1)\right] .$$

(1 und 2 entsprechen allen Koordinaten der Teilchen 1 und 2. Wie findet man die entsprechenden Zustände für mehrere Teilchen?

In einem System aus $N$ Teilchen sind $N!$ verschiedene Vertauschungen der Teilchen möglich. Die Funktion zu einer bestimmten Permutation der Teilchen kann man aus der ursprunglichen Funktion $\psi (1,2,...,N)$ durch fortgesetzte Vertauschung von Teilchenpaaren bekommen. $\hat{P}_{\nu }\psi (1,2,...,N)$ entspricht dem Operator der dem Vertauschen von $\nu$ Paare entspricht (dem kann man explizit durch die Summe über der Paarvertauschungsoperatoren ausdrucken). Die Symmetrische WF ist dann

$$\psi _{s}=A\sum_{\nu }\hat{P}_{\nu }\psi (1,2,...,N)$$

und

$$\psi _{a}=B\sum_{\nu }(-1)^{\nu }\hat{P}_{\nu }\psi (1,2,...,N).$$

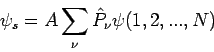
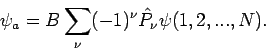
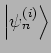Als Basis in den entsprechenden Hilberträumen kann man die Produktbasis der Einteilchenzuständen benutzen: Aus der von nichtwechselwirkenden Teilchen anfangend, kann man die Basis der Einteilchenzuständen $\left\vert \psi _{n}^{(i)}\right\rangle$ benutzen, so dass, z.B.

$$H_{i}\left\vert \psi _{n}^{(i)}\right\rangle =E_{n}\left\vert \psi _{n}^{(i)}\right\rangle$$

(alle $H_{i}$ sind die Operatoren, die von den Koordinaten der Teilchen $i$ für alle $i$ in gleicherweise abhängen, da die Teilchen identisch sind und nicht wechselwirken!).

$$\left\vert \psi _{n_{1},n_{2},}...\right\rangle =\left\vert ... ...\right\rangle ...\left\vert \psi _{n_{N}}^{(N)}\right\rangle .$$

Für Bosonen entsprechen die Basisfunktionen dann den symmetrisierten Produkten

$$\left\vert \psi _{n_{1},n_{2},}...\right\rangle _{s}=\frac{1... ...\right\rangle ...\left\vert \psi _{n_{N}}^{(N)}\right\rangle .$$

Das antisymmetrisierte Produkt für die Fermionen

$$\left\vert \psi _{n_{1},n_{2},}...\right\rangle _{a}=\frac{1... ...}\right\rangle ...\left\vert \psi _{n_{N}}^{(N)}\right\rangle$$

lasst sich in Form einer Determinante schreiben:

$$\left\vert \psi _{n_{1},n_{2},...n_{N}}\right\rangle _{a}=\f... ...vert \psi _{n_{N}}^{(N)}\right\rangle \end{array}\right\vert$$ (55)

(die SLATER-Determinante). Die Vorzeichenänderung der WF bei der Vertauschung eines beliebeigen Teilchenpaares folgt aus dem Vorzeichenwechsel der Determinante bei der Vertauschung zweier Spalten.

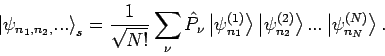
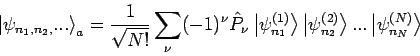
Aus der Form der Gl.(55) folgt das PAULI-Prinzip: Ein System aus gleichartigen Fermionen kann sich nicht in einem Zustand befinden, der durch eine WF Gl.(55) mit zwei oder mehreren gleichen Einteilchenzuständen beschrieben wird: Wenn unter Einteilchenzuständen $n_{1},n_{2},...,n_{N}$ auch nur zwei gleich sind, dann verschwindet die Determinante identisch.