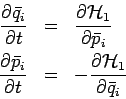Next: Kanonische Transformation.
Up: Klassische Theorie des Wasserstoffatoms
Previous: Klassische Theorie des Wasserstoffatoms
Contents
(Hier wird angenommen, dass
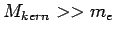 ). Am besten zu beschreiben
in Polarkoordinaten. Übergang von
). Am besten zu beschreiben
in Polarkoordinaten. Übergang von
zu
mit
Die Hamiltonfkt. des Problems (in Kugelkoordinaten) ist
mit
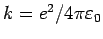 . Die Koordinate
. Die Koordinate 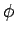 ist zyklisch,
d.h.
ist zyklisch,
d.h.
daher ist der dazugehörige Impuls
konstant (erhalten). Dieser Impuls fällt mit der 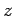 -Komponente
-Komponente 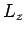 des Drehimpuls zusammen. (Bewegungsintegral). Die Bewegung erfolgt in einer
festen Ebene. Die Energie
des Drehimpuls zusammen. (Bewegungsintegral). Die Bewegung erfolgt in einer
festen Ebene. Die Energie 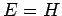 ist auch ein Bewegungsintegral.
ist auch ein Bewegungsintegral.
Eleganteste Lösung für die periodische Bewegung: Übergang zu
Wirkung-Winkel Variablen, die neue verallg. Koordinaten und Impulse
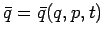 ,
,
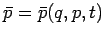 und eine neuen
Hamiltofkt.
und eine neuen
Hamiltofkt.
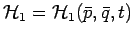 .
.
Die Winkelvariablen sind zyklisch und definieren entsprechende Frequenzen,
die dazugehörige verallgemeinerte Impulse (Wirkungsvariablen) sind
konstant, d.h. die stellen die Bewegungsintegrale dar:
Prof. Igor Sokolov
2005-02-14
![]() ). Am besten zu beschreiben
in Polarkoordinaten. Übergang von
). Am besten zu beschreiben
in Polarkoordinaten. Übergang von
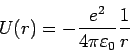
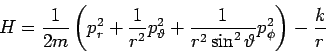
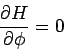
![]() ,
,
![]() und eine neuen
Hamiltofkt.
und eine neuen
Hamiltofkt.
![]() .
.