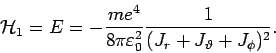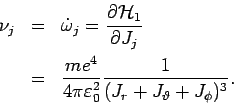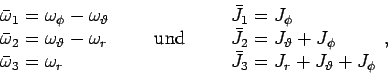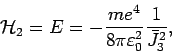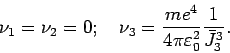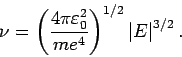Next: Bohr'sche Quantenhypothese.
Up: Klassische Theorie des Wasserstoffatoms
Previous: Das Kepler-Problem
Contents
Die Transformation von alten zu neuen Variablen erfolgt über eine
erzeugende Funktion
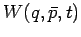 so dass
so dass
Da
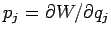 , erfüllt
, erfüllt 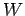 die HAMILTON-JACOBI-Differenzialgleichung
die HAMILTON-JACOBI-Differenzialgleichung
Die Gl. bestimmt die 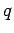 -abhängigkeit der Erzeugende; die neuen Impulse
sind nicht eindeutig festgelegt (
-abhängigkeit der Erzeugende; die neuen Impulse
sind nicht eindeutig festgelegt (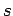 Integrationskonstanten
Integrationskonstanten
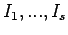 , zusammengefasst in Wektor
, zusammengefasst in Wektor 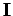 ) und können zweckmässig
gewählt werden. In unserem Fall
) und können zweckmässig
gewählt werden. In unserem Fall
Variablentrennung:
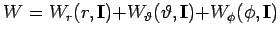 . Da
. Da 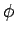 shon zyklisch ist, ist
shon zyklisch ist, ist
identisch mit 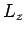 . Daher:
. Daher:
potentielle + ''zentrifugale'' Energie. Sortieren, 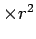 multiplizieren:
multiplizieren:
Linke Seite hängt nur von 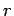 ab; rechte Seite nur von
ab; rechte Seite nur von 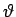
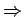 beide müssen konstant sein.
beide müssen konstant sein.
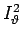 ist mit dem Quadrat des Drehimpulses identisch:
ist mit dem Quadrat des Drehimpulses identisch:
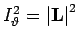 . Letzlich,
. Letzlich,
Die neue verallg. Impulse sind die Funktionen der Integrationskonstanten 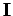 . Zweckmässig ist die Wahl von Wirkungsvariablen
. Zweckmässig ist die Wahl von Wirkungsvariablen 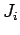 als
verallg. Impulse:
als
verallg. Impulse:
(Integral ''hin'' und ''zurück'' über die Periode der Bewegung).
Dieser Wahl wird klar, wenn wir die Eigenschaften der adiabatischen
Invarianten diskutieren (siehe Abschnitt...). Die Winkelvariablen sind
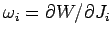 . In unserem Fall
. In unserem Fall
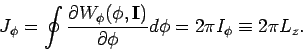 |
(2) |
ist elementar. Ferner,
Da die Periode der 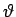 -Bewegung erfolgt zwischen der Umkehrpunkten, wo
-Bewegung erfolgt zwischen der Umkehrpunkten, wo
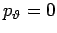 , d.h.
, d.h.
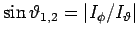 ergibt die Integration (Tabellenintegral) dann
ergibt die Integration (Tabellenintegral) dann
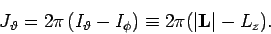 |
(3) |
Die letzte Wirkungsvariable ist dann
mit
(Potenzial der Coulomb'schen und ''zentrifugalen'' Kräfte). Die
Umkehrpunkte sind die Nullstellen von 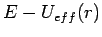 . Die Integration (sieh
Nolting, Band.2, §3.5.3) ergibt:
. Die Integration (sieh
Nolting, Band.2, §3.5.3) ergibt:
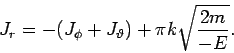 |
(4) |
(gebunden sind nur die Zustände mit 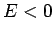 , sonnst ist die Bewegung nicht
mehr finit).
, sonnst ist die Bewegung nicht
mehr finit).
Die Gl. (2), (3) und (4) lassen sich nach 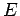 auflösen:
auflösen:
Die Frequenzen sind, offensichtlich, entartet
Die Entartung ist sehr störend, kann aber durch eine nochmalige
kanonische Transformation
aufgehoben werden, mir der erzeugenden Funktion
Neue Variablen sind:
die neue(ste) Hamilton-Fkt. ist
und die Frequenzen sind
Man nennt 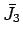 eine Eigenwirkungsvariable: Die
zugehörige Frequenz ist nicht Null und nicht entartet. Für die
entsprechende Frequenz
eine Eigenwirkungsvariable: Die
zugehörige Frequenz ist nicht Null und nicht entartet. Für die
entsprechende Frequenz 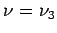 kann man auch schreiben
kann man auch schreiben




Next: Bohr'sche Quantenhypothese.
Up: Klassische Theorie des Wasserstoffatoms
Previous: Das Kepler-Problem
Contents
Prof. Igor Sokolov
2005-02-14
![]() so dass
so dass
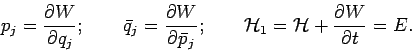
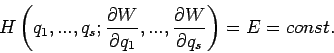
![\begin{displaymath}
\frac{1}{2m}\left[ \left( \frac{\partial W}{\partial r}\righ...
...\partial W}{\partial \phi }\right)
^{2}\right] -\frac{k}{r}=E
\end{displaymath}](img127.png)
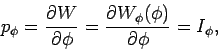
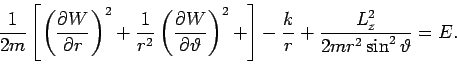
![\begin{displaymath}
\frac{r^{2}}{2m}\left( \frac{\partial W}{\partial r}\right) ...
...ht) ^{2}+%
\frac{I_{\phi }^{2}}{\sin ^{2}\vartheta }\right] .
\end{displaymath}](img132.png)
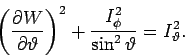
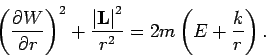
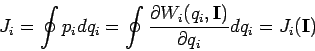
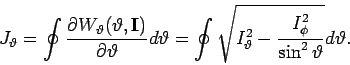
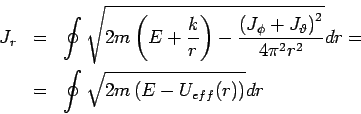
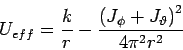
![]() auflösen:
auflösen: