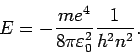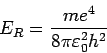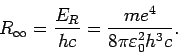Next: Das Korrespondenzprinzip
Up: Klassische Theorie des Wasserstoffatoms
Previous: Kanonische Transformation.
Contents
(BOHR'sche) Quantenhypothese: Bei einer
Eigenwirkungsvariable 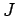 ist die Systembewegung nur auf solchen Bahnen
zugelassen, für die
ist die Systembewegung nur auf solchen Bahnen
zugelassen, für die
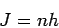 |
(5) |
(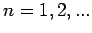 ) gilt.
) gilt.
Infolgedessen, für das Wasserstoffatom
Die Kombination
definiert die Rydberg-Energie.
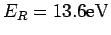 . Daher ist die
Rydberg-konstante für das Wasserstoffatom
. Daher ist die
Rydberg-konstante für das Wasserstoffatom
Dieser Wert gilt für den unendlich schweren Kern. Für Wasserstoff
(reduzierte Masse
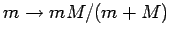 ,
, 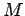 -Kernmasse) ist
-Kernmasse) ist
Prof. Igor Sokolov
2005-02-14
![]() ist die Systembewegung nur auf solchen Bahnen
zugelassen, für die
ist die Systembewegung nur auf solchen Bahnen
zugelassen, für die