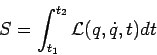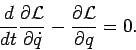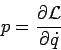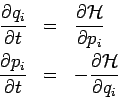Next: Lichtwellen
Up: Das Ende der klassichen
Previous: Klassische Doktrin:
Contents
- Für ein Teilchen genügen 2 Variablen (Koordinate und
Geschwindigkeit / Impuls) pro Raumdimension. Insgesamt ist der Zustand des
Systems aus mehreren Teilchen (
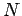 Koordinaten) als Punkt in Phasenraum
der (verallgemeinerten) Koordinaten/Impulse gegeben:
Koordinaten) als Punkt in Phasenraum
der (verallgemeinerten) Koordinaten/Impulse gegeben:
LAGRANGE'sche Formulierung und Extremale Wirkung: Die
Lagrange-Funktion
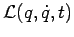 (typischerweise
(typischerweise
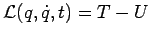 ,
, 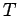 -kinetische Energie,
-kinetische Energie, 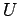 -potenziele Energie) definiert
das Integral
-potenziele Energie) definiert
das Integral
(Wirkung), das entlang der ''richtigen'' Trajektorie 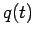 extremal
(minimal) ist. Daher folgen die Bewegungsgl:
extremal
(minimal) ist. Daher folgen die Bewegungsgl:
Z.B. ein Teilchen in einem Potential 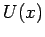 :
:
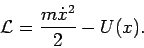 |
(1) |
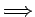
oder
Wichtige Bemerkung:
ist ein (verallgemeinertes) Impuls. Z.B. für (1) erhälte man
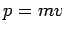 .
.
- HAMILTON'sche Formulierung: (
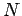 Koordinaten) startet von
einer Hamiltonfunktion
Koordinaten) startet von
einer Hamiltonfunktion
Die Hamilton'sche Bewegungsgleichungen
Besonders vorteilhaft für konservative Systeme: in diesem Fall ist
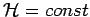 und ist gleich der Gesamtenergie des Systems.
und ist gleich der Gesamtenergie des Systems.
- Für die Felder (z.B. Elektromagnetismus)
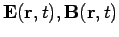 ist Lagrange'sche Formulierung möglich.
ist Lagrange'sche Formulierung möglich.
- Theorie der Wechselwirkung der Teilchen (Elektronen, J.J. Thomson,
1897) mit EM Felder (Lorentz)




Next: Lichtwellen
Up: Das Ende der klassichen
Previous: Klassische Doktrin:
Contents
Prof. Igor Sokolov
2005-02-14