



Next: Interferenz und Beugung
Up: Das Ende der klassichen
Previous: Grundriss der klassischen Mechanik
Contents
Aus den Maxwell-Gleichungen für die Feldvariablen folgt die Wellengleichung
wobei 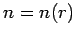 die Brechzahl des Mediums und
die Brechzahl des Mediums und 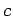 die Lichtgeschwindigkeit
des Vakuums ist (lineare Medien!).
die Lichtgeschwindigkeit
des Vakuums ist (lineare Medien!). 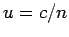 ist die Lichtgeschwindigkeit in
Medium, sog. Phasengeschwindigkeit. Für
ist die Lichtgeschwindigkeit in
Medium, sog. Phasengeschwindigkeit. Für 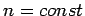 ist die spezielle
Lsg. eine ebene Welle
ist die spezielle
Lsg. eine ebene Welle
mit
Daraus folgen die Ausdrücke für 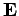 und
und 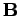 . Die Welle
jeder anderen beliebigen Form kann als Superposition ebener Wellen
dargestellt werden:
. Die Welle
jeder anderen beliebigen Form kann als Superposition ebener Wellen
dargestellt werden:
Die Brechzahl kann von 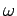 (oder
(oder 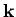 ) abhängig sein, was
die Dispersion verursacht. Die Abhängigkeit
) abhängig sein, was
die Dispersion verursacht. Die Abhängigkeit 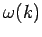 wird
das Dispersionsgesetz genannt.
wird
das Dispersionsgesetz genannt.
Bemerkung: Die komplexe Schreibeweise erleichtet mathematische Handhabung.
Tatsächlich sind alle Potenziale und Felder reel, so dass z.B.
![$\mathbf{E}(\mathbf{r},t)=\mathrm{Re} \left[ \mathbf{E}_{0}(\mathbf{r},t)e^{i\left(
\mathbf{kr}-\omega t+\phi \right) }\right] $](img43.png) . Die Energiedichte
. Die Energiedichte
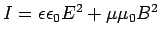 ist in der komplexen Schreibeweise durch
ist in der komplexen Schreibeweise durch
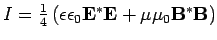 oder
oder
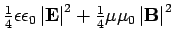 gegeben.
gegeben.
Subsections
Prof. Igor Sokolov
2005-02-14
![]() . Die Energiedichte
. Die Energiedichte
![]() ist in der komplexen Schreibeweise durch
ist in der komplexen Schreibeweise durch
![]() oder
oder
![]() gegeben.
gegeben.