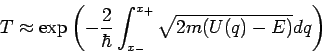Betrachten wir ein folgendes Beispiel der Streuzustände im entarteten
kontinuierlichen Spektrum: Das Potential ![]() entspricht einem
Potentialwall von der Höhe
entspricht einem
Potentialwall von der Höhe ![]() und der Breite
und der Breite ![]() .
.
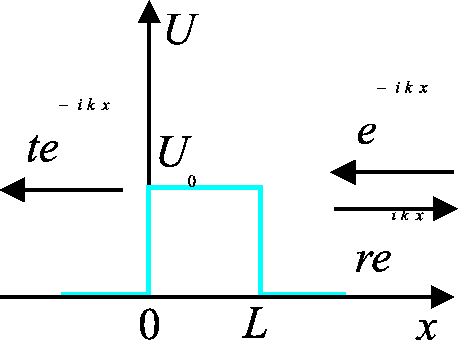
Die hier betrachtete Situation entspricht einem Wellenpaket mit den
Wellenzahlen, die scharf um ![]() lokalisiert sind; im Koordinatenraum muss
so ein Paket sehr breit sein. Wesentlich ist, dass diese Breite größer ist als
lokalisiert sind; im Koordinatenraum muss
so ein Paket sehr breit sein. Wesentlich ist, dass diese Breite größer ist als ![]() . Praktisch haben wir hier mit eine ebene Welle zu tun. Damit
wird die physikalische Situation auf die Betrachtung der Eigenzustände
der Schrödinger-Gl. reduziert. Das Bild der Wellenpakete braucht man nur
für die Interpretation der Resultate.
. Praktisch haben wir hier mit eine ebene Welle zu tun. Damit
wird die physikalische Situation auf die Betrachtung der Eigenzustände
der Schrödinger-Gl. reduziert. Das Bild der Wellenpakete braucht man nur
für die Interpretation der Resultate.
Die entsprechende ebene Welle von der Amplitude ![]() kann das Potential
durchdringen und / oder reflektiert werden. Die reflektierte Welle hat
ausserhalb des Walls den Wellenvektor
kann das Potential
durchdringen und / oder reflektiert werden. Die reflektierte Welle hat
ausserhalb des Walls den Wellenvektor ![]() von dem gleichen Betrag wie die
anfallende Welle, und die Amplitude
von dem gleichen Betrag wie die
anfallende Welle, und die Amplitude ![]() ; die durchgegangene Welle auf
der anderen Seite des Walls hat die Amplitude
; die durchgegangene Welle auf
der anderen Seite des Walls hat die Amplitude ![]() . In die Sprache der
Wellenpakete übersetzt, sagt das, dass der reflektierte Teil des
Pakets (von praktisch gleicher räumlicher Ausdehnung) hat die Amplitude im
Maximum
. In die Sprache der
Wellenpakete übersetzt, sagt das, dass der reflektierte Teil des
Pakets (von praktisch gleicher räumlicher Ausdehnung) hat die Amplitude im
Maximum ![]() , das durchgegangene Paket auf der anderen Seite des Walls hat die
Amplitude im Maximum
, das durchgegangene Paket auf der anderen Seite des Walls hat die
Amplitude im Maximum ![]() . Die Wahrscheinlichkeit, ein Teilchen rechts
(links) von dem Wall zu finden ist proportional zu
. Die Wahrscheinlichkeit, ein Teilchen rechts
(links) von dem Wall zu finden ist proportional zu
![]() bzw.
bzw.
![]() , siehe Bild.
, siehe Bild.
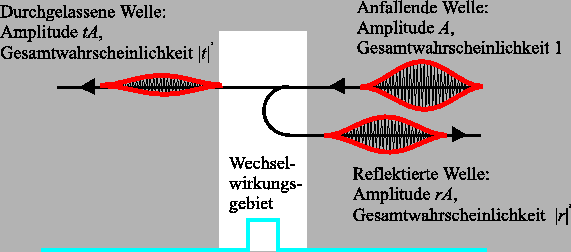
Hier unterscheidet man 2 Fälle:
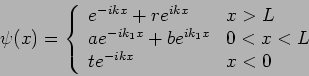
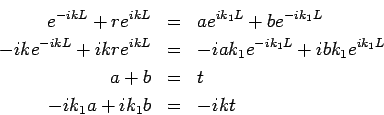
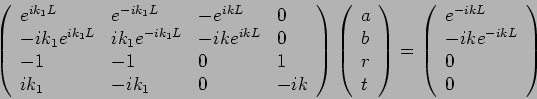
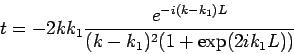
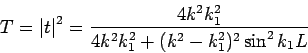
Wichtig: Im Quantenfall (abgesehen von die Situationen mit
![]() mit
mit ![]() ) wird das Teilchen mit einer gewissen
Wahrscheinlichkeit reflektiert, was im klassischen Fall bei
) wird das Teilchen mit einer gewissen
Wahrscheinlichkeit reflektiert, was im klassischen Fall bei ![]() nie
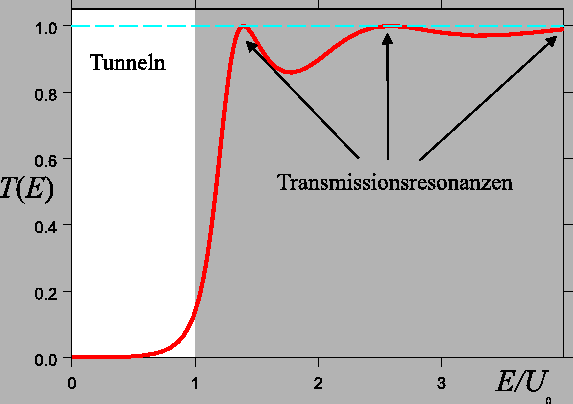
der Fall ist. Das Gesamtverhalten zeigt Resonanzen, siehe Bild.
nie
der Fall ist. Das Gesamtverhalten zeigt Resonanzen, siehe Bild.
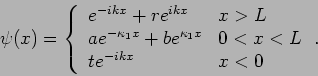
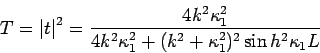
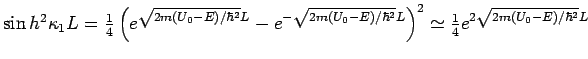 sehr groß, und
sehr groß, und
Das Gesamtverhalten von ![]() für
für
![]() siehe
Bild.
siehe
Bild.
Bemerkung: i.A. für den Potentialwall beliebiger Form ![]() (
(
![]() ) und für die Energien
) und für die Energien ![]() für welche
die Gleichung
für welche
die Gleichung ![]() nur 2 Wurzel hat (2 klassische Umkehrpunkte der
Bewegung
nur 2 Wurzel hat (2 klassische Umkehrpunkte der
Bewegung ![]() ) gilt:
) gilt: