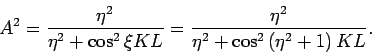Next: Interpretation der Resultate
Up: Streuzustände (kontinuierliches Spektrum)
Previous: Beispiel 1: Das Tunnel-Effekt
Contents

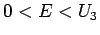
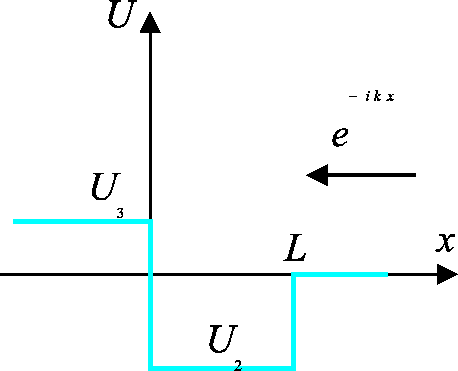
Das Verhalten der Wellenfunktion:
(Da es für 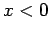 keine nach links laufende Welle gibt, sind die
Amplituden der nach links und nach rechts laufenden Wellen für
keine nach links laufende Welle gibt, sind die
Amplituden der nach links und nach rechts laufenden Wellen für 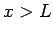 gleich. Es ist vernünftig, die Koeffiziente in 2 bzw. 3 Zeile als
gleich. Es ist vernünftig, die Koeffiziente in 2 bzw. 3 Zeile als
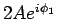 und
und
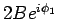 zu schreiben, da die Phasen
wegkürzen!) mit
zu schreiben, da die Phasen
wegkürzen!) mit
Für die vorgegebene Amplitude der einfallenden Welle (hier 1) haben die
Gleichungen immer 1 Lösung. Das Spektrum is kontinuierlich und nicht
entartet. Die Phasen folgen aus der Bedingung der Kontinuität der
logarithmischen Ableitung, die Vorfaktoren 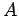 und
und 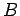 aus der
Kontinuität von
aus der
Kontinuität von 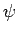 selbst. Man bekommt:
selbst. Man bekommt:
und
Wir betrachten hier nur den einfachsten Spezialfall
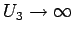 (mit
(mit
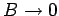 ) und führen
) und führen
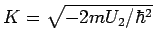 und
und
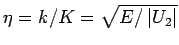 und
und 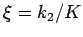 . Es gilt
. Es gilt
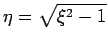 . Dann gilt:
. Dann gilt:
und
(Bemerkung:
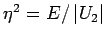 ist dimensionslose Energie!).
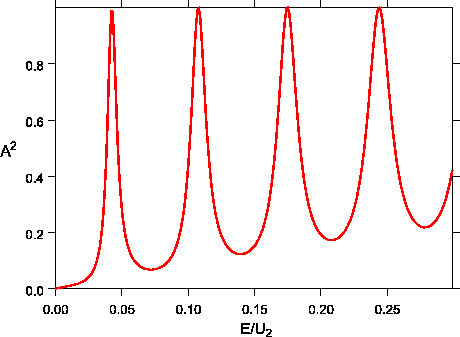
Die Amplitude zeigt Resonanzen für
ist dimensionslose Energie!).
Die Amplitude zeigt Resonanzen für
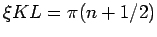 . Dabei ist
. Dabei ist
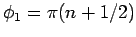 . Hier ist das Bild für
. Hier ist das Bild für 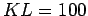 .
.




Next: Interpretation der Resultate
Up: Streuzustände (kontinuierliches Spektrum)
Previous: Beispiel 1: Das Tunnel-Effekt
Contents
Prof. Igor Sokolov
2005-02-14

![]()
![]()
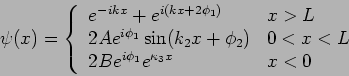
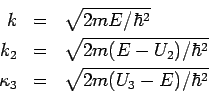
![\begin{displaymath}
\phi _{1}=-kL-\frac{\pi }{2}+Arc\tan \left[ \frac{k}{k_{2}}\...
...eft(
k_{2}L+Arc\tan \frac{k_{2}}{\kappa _{3}}\right) \right] .
\end{displaymath}](img613.png)
![\begin{displaymath}
\phi _{1}=-\frac{\pi }{2}+Arc\tan \left[ \frac{\eta }{\xi }\tan \left( \xi
KL\right) \right]
\end{displaymath}](img619.png)