Interpretation der Resultate

Vergleichen wir die Bewegung eines von rechts einfallenden Wellenpakets (Wellenvektoren um $k$) mit der Bewegung eines klassischen Teilchen.

Das klassische Teilchen bewegt sich für $x>L$ mit einer konstanten Geschwindigkeit $v=-\sqrt{2mE}=-(\hbar K/m)\eta$, erfährt unendlich große Beschleunigung in $x=L$, bewegt sich mit einer konstanten Geschwindigkeit $v_{2}=-\sqrt{2m(E-U_{2})}=-(\hbar K/m)\sqrt{1+\eta ^{2}}$ bis zum Punkt $x=0$, diese Bewegung kehrt sich um am Punkt $x=0$, das Teilchen bewegt sich mit Geschwindigkeit $-v_{2}$ bis zum Punkt $x=L$, und dann weiter nach rechts mit der Geschwindigkeit $-v$. Die Zeit, die das Teilchen bei $0<x<L$ verbringt ist $\tau _{kl}=2L/v_{2}$. Die Wahrscheinlichkeit, ein Teilchen innerhalb dieses Intervalls bei einer zufälligen Beobachtung zu finden ist $P\symbol{126}1/\tau _{kl}$.

Die Bewegung von Quantensystem entspricht weit von der Mulde der Superposition von 2 Wellenpaketen ($\Delta k$ klein!): der einfallenden Welle

$$\Psi (x,t)=\int_{0}^{\infty }f(k^{\prime }-k)e^{-ik^{\prime }x-i\omega t}dk^{\prime }$$

und der reflektierten Welle

$$\Psi _{r}(x,t)=-\int_{0}^{\infty }f(k^{\prime }-k)e^{ik^{\prime }x+2i\phi (k)-i\omega t}dk^{\prime }$$

mit $\omega =E/\hbar$ (da alle Teilchen, die von rechts kommen am Ende reflektiert wurden, sind die Beträge der Funktionen $f$ in beiden Ausdrücken gleich, vgl. Amplituden der 2 Wellen in $\psi (x)$). In der einfallenden Welle werden nur Teilchen mit $p<0$ berücksichtigt, die sich nach links bewegen. Die Zentren der Wellenpackete bewegen sich gemäß

$$\frac{d\varphi (x,t)}{dk}=0$$

wobei $\varphi (x,t)=-ik^{\prime }x-i\omega t$ bzw. $\varphi (x,t)=ik^{\prime }x+2i\phi _{1}(k)-i\omega t$ sind die Phasen der Wellen. Die Mitte des einfallenden Wellenpakets vollführt die Bewegung die dem des klassichen Teilchens ähnlich ist: sein Zentrum hat die Koordinate $% X_{1}=-vt$ mit $v=d\omega /dk$ ($t=0$ entspricht dem ''Zeitpunkt'' der Streuung). Die Mitte des reflektierten Pakets bewegt sich gemäß

$$X_{r}=vt-2(d\phi _{1}/dk).$$

Da wir die Situation mit scharf definiertem $k$ betrachten, ist das Paket sehr breit ($\gg L$). Innerhalb der Mulde gilt $X=\pm vt-2(d\phi _{1}/dk)$. Aus den Koordinaten kann man die ''Zeit innerhalb der Mulde ablesen'' Diese Zeit ist von der Größenordnung von $t_{2}-t_{1}$ mit $% X_{1}(t_{1})=X_{r}(t_{r})=L$. Daher

$$2v\tau _{qu}=2(d\phi _{1}/dk)$$

so dass

$$\tau _{qu}=\frac{1}{v}(d\phi _{1}/dk).$$

Im Resonanzfall hat man dann $\tau _{qu}\simeq \tau _{kl}/\eta$; zwischen der Resonanzen $\tau _{qu}\simeq \tau _{kl}\eta$.

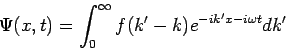
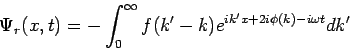
Bemerkung: Da in der Quantenmechanik die Position des Teilchens, besonders bei kleinem $\Delta k$, nich scharf definiert ist, kann diese Zeit $% \tau$ nur probabilistisch interpretiert werden, in etwa wie $P\sim 1/\tau$. Die Interpretationen, wie die oben diskutierte, sind sehr grob!

$\bullet$ $U_{3}<E$. In diesem Fall ist die Wellenfunktion im Bereich $x<0$ gleich $c_{1}e^{ik_{3}x}+c_{2}e^{-ik_{3}x}$: es gibt einen zusätzlichen Parameter. Jeder Energie entsprechen in diesem Fall 2 Lösungen (bis zu Normierung). Siehe Hausaufgabe!