



Next: Kronig-Penney-Modell
Up: Bewegung in periodischem Potential
Previous: Bewegung in periodischem Potential
Contents
ausgedrückt wird. Wir beschränken uns hier zunächst auf das
eindimensionale Problem. Man hat eine SGl. in einem periodischen Potential 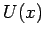 so das
so das 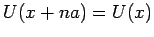 ,
,
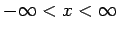 ,
, 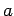 ist die
Gitterkonstante. Der Hamilton-Operator des Systems
ist die
Gitterkonstante. Der Hamilton-Operator des Systems
ist invariant gegen die Translation um 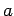 :
:
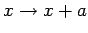 . Solche
Invarianz soll dementsprechend für alle beobachtbare Größen
gelten. Die Wellenfunktion selbst ist nicht beobachtbar, somit können
. Solche
Invarianz soll dementsprechend für alle beobachtbare Größen
gelten. Die Wellenfunktion selbst ist nicht beobachtbar, somit können 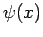 und
und 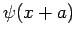 unterschiedlich sein; das Betragsquadrat der
Wellenfunktion ist hingegen beobachtbar, so dass
unterschiedlich sein; das Betragsquadrat der
Wellenfunktion ist hingegen beobachtbar, so dass
Damit können 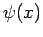 und
und 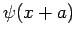 sich nur um einen reinen
Phasenfaktor
sich nur um einen reinen
Phasenfaktor 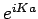 unterscheiden:
unterscheiden:
Da 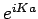 periodisch ist, können wir stets
periodisch ist, können wir stets
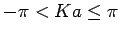 wählen. Die Lsg. ist damit durch eine zusätzliche Wellenzahl
wählen. Die Lsg. ist damit durch eine zusätzliche Wellenzahl 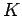 gekennzeichnet:
gekennzeichnet:
Das ist für jedes 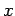 nur dann möglich, wenn
nur dann möglich, wenn
mit 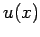 periodisch,
periodisch,
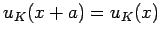 . Wenn
. Wenn
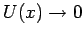 , gilt
, gilt
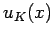 , und die Wellenfunktionen sind die ebene Wellen; andererseits sind
sie durch eine periodische Funktion moduliert. Die Fkt.
, und die Wellenfunktionen sind die ebene Wellen; andererseits sind
sie durch eine periodische Funktion moduliert. Die Fkt. 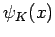 ist
nicht im eigentlichen Sinne normierbar, und gehört dem kontinuierlichen
Spektrum an. In einem endlichen Kristall der Länge
ist
nicht im eigentlichen Sinne normierbar, und gehört dem kontinuierlichen
Spektrum an. In einem endlichen Kristall der Länge 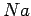 kann die Normierung
durch periodische Randbedingung erzwungen werden:
kann die Normierung
durch periodische Randbedingung erzwungen werden:




Next: Kronig-Penney-Modell
Up: Bewegung in periodischem Potential
Previous: Bewegung in periodischem Potential
Contents
Prof. Igor Sokolov
2005-02-14
![]() so das
so das ![]() ,
,
![]() ,
, ![]() ist die
Gitterkonstante. Der Hamilton-Operator des Systems
ist die
Gitterkonstante. Der Hamilton-Operator des Systems