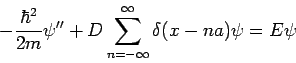Next: Harmonischer Oszillator
Up: Bewegung in periodischem Potential
Previous: Bloch-Theorem
Contents
Als Beispiel betrachten wir das Modell mit periodisch angeordnete 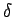 -Potentialen:
-Potentialen:
(periodisches Potential mit einer Gitterkonstante 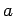 ). Die Eigenschaften
des Modells sind bei
). Die Eigenschaften
des Modells sind bei 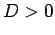 und bei
und bei 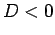 weitgehend gleich; wir betrachten
hier nur den Fall
weitgehend gleich; wir betrachten
hier nur den Fall 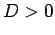 (
(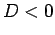 : siehe Hausaufgabe!).
: siehe Hausaufgabe!).
In der Situation 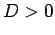 gibt es keine nichtverschwindenden Ls'gen
gibt es keine nichtverschwindenden Ls'gen
der SGl mit 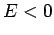 . Zwischen der
. Zwischen der 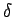 -Funktionen ist das Teilchen frei;
die Lösung des SGl ist eine Superposition ebenen Wellen:
-Funktionen ist das Teilchen frei;
die Lösung des SGl ist eine Superposition ebenen Wellen:
Im 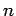 -ten Intervall ist es zweckmässig zu schreiben
-ten Intervall ist es zweckmässig zu schreiben
Aus dem Bloch-Theorem
folgt, dass nur 2 der Koeffizienten 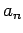 und
und 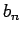 unabhängig
sind:
unabhängig
sind:
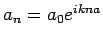 ,
,
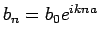 . Wir benutzen jetzt
unsere Aussage über das Verhalten einer WF im
. Wir benutzen jetzt
unsere Aussage über das Verhalten einer WF im 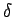 -Potential: Bei
-Potential: Bei 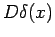 ist die Wellenfunktion stetig
ist die Wellenfunktion stetig
und ihre Ableitung erfährt einen endlichen Sprung,
Solch eine ''Nahtbedingung'' soll an jedem 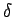 -Peak erfüllt
werden. Daher:
-Peak erfüllt
werden. Daher:
(Kontinuität bei 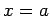 ) und
) und
Insgesamt, ausgedrückt durch 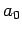 und
und 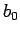 bekommt man:
bekommt man:
Die Bedingung des Verschwindens der Hauptdeterminanten ergibt
Schlußfolgerungen:




Next: Harmonischer Oszillator
Up: Bewegung in periodischem Potential
Previous: Bloch-Theorem
Contents
Prof. Igor Sokolov
2005-02-14
![]() -Potentialen:
-Potentialen:
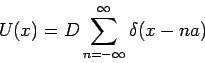
![]() gibt es keine nichtverschwindenden Ls'gen
gibt es keine nichtverschwindenden Ls'gen